练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．已知a1=$\frac{1}{4}（1-\frac{1}{3}）$，a2=$\frac{1}{4}（\frac{1}{3}-\frac{1}{5}）$，a3=$\frac{1}{4}（\frac{1}{5}-\frac{1}{7}）$，a4=$\frac{1}{4}（\frac{1}{7}-\frac{1}{9}）$…依此类推，则a1+a2+a3+…+a100的值为$\frac{50}{201}$．

    分析 根据已知条件发现规律：${a}_{n}=\frac{1}{4}（\frac{1}{2n-1}-\frac{1}{2n+1}）$．

    解答 解：a1+a2+a3+…+a100=$\frac{1}{4}$（1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$$+\frac{1}{7}$-$\frac{1}{9}$-…+$\frac{1}{1999}-\frac{1}{2001}$）=$\frac{1}{4}$（1-$\frac{1}{2001}$）=$\frac{500}{2001}$．
    故答案为：$\frac{50}{201}$．

    点评 此题考查数字的变化规律，根据所求出的数，观察出n变化规律是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=10，CD=8，那么线段AE的长为（　　）
    A．5B．4C．3D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．下列根式中，与$\sqrt{2}$是同类二次根式的是（　　）
    A．$\sqrt{24}$B．$\sqrt{\frac{3}{2}}$C．$\sqrt{12}$D．$\sqrt{18}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

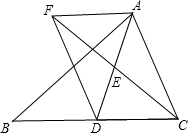    11．已知：如图，在△ABC中，D是BC边上的一点，连接AD，取AD的中点E，过点A作BC的平行线与CE的延长线交于点F，连接DF．
    （1）求证：△AEF≌△DEC；
    （2）若CF=AD，试判断四边形AFDC是什么样的四边形？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知，∠EPF的角平分线上有一点O，以点0为圆心的圆与角的两边分别交于A，B和C，D．易证：AB=CD．
    当点P在⊙O外（如图二），点P在⊙O内，（如图三）的位置时，请你猜想并写出AB与CD的数量关系？并选择其中一种情况加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

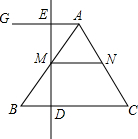    8．如图，△ABC中，点M是AB边的中点，点D是BC边上一个动点，直线DM交射线AG于点E，AG∥BC．
    （1）求证：ME=MD；
    （2）N是AC的中点，且MN=5．
    填空：①若AB=AC，当BD=5时，四边形AEBD是矩形；
    ②若AB⊥AC，当BD=5时，四边形AEBD是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．观察下列各等式：$\frac{1}{2×4}$=$\frac{1}{4×2}$，$\frac{1}{2×4}$+$\frac{1}{4×6}$=$\frac{2}{4×3}$，$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$=$\frac{3}{4×4}$，…
    （1）猜想并写出第n个等式．
    （2）这个等式的结果能等于$\frac{19}{80}$吗？若能，请写出这个等式；若不能，请分析原因．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

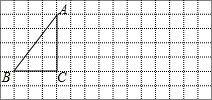    9．如图，方格纸中的每个小方格都是边长为1个单位长度的正方形．
    ①画出将Rt△ABC向右平移4个单位长度后的Rt△A1B1C1；
    ②再将Rt△A1B1C1绕点C1顺时针旋转90°，画出旋转后的Rt△A2B2C2，并求出旋转过程中线段A1C1所扫过的面积（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．有“安徽第一楼”之称的安徽省国际金融大厦是具有国际化、专业化、现代化的金融服务场所，它由高度不同的两座楼组成，如图，从左楼丁C处测得右楼楼顶A处的仰角为60°，在左楼楼底D处测得A处的仰角为75°，已知左楼CD高126米，请你利用已知数据估算右楼AB的高．（结果精确到1米，$\sqrt{3}$≈1.7）

    查看答案和解析>>

    同步练习册答案