

���� ��1��������չ����A��x��y��Ϊ��P������һ�㣬����AP=r�������Ķ������е�����֮����빫ʽ���������P�ķ��̣�
��2���ۺ�Ӧ�ã����жϳ���PAB=90�㣬������ͬ�����Ե�Բ�ܽ���ȵó���OBP=��PAO=��POA������tan��OBP=$\frac{OP}{OB}$=$\frac{3}{4}$����P����������OP��OB������Q��QE��OB��E���ó�QE�ǡ�POB����λ���ɵó����ۣ�
��� �⣺��1��������չ����A��x��y��Ϊ��P������һ�㣬
��P��a��b�����뾶Ϊr��
��AP2=��x-a��2+��y-b��2=r2��
�ʴ�Ϊ��x-a��2+��y-b��2=r2��
��2���ۺ�Ӧ�ã�
��ͼ��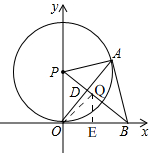
������ڵ��ĵ�O��P��A��B���붼��ȵĵ�Q��
������O��P��A��B�ĵ��ڡ�Q�ϣ�
��OQ=OP=OB
�ߡ�P��x��������ԭ��O��
��PO=PA����POB=90�㣬
��PB�ǡ�Q��ֱ����
���PAB=90��
�ڡ�P�У�PO=PA��
���POA=��PAO��
�ߵ�O��P��A��B�ڡ�Q�ϣ�
���PBO=��PAB��
���PBO=��POA��
��tan��POA=$\frac{3}{4}$��
��tan��PBO=$\frac{3}{4}$��
��P��0��3����
��OP=3��
��Rt��POB��OP=3��tan��PBO=$\frac{OP}{OB}$=$\frac{3}{4}$��
��OB=4��PB=5��
��OQ=BQ=PQ=$\frac{1}{2}$PB=$\frac{5}{2}$��
����Q��QE��OB��E��
��QE��OP��
��PB�ǡ�Q��ֱ����
��PQ=BQ��
��QE�ǡ�POB����λ�ߣ�
��QE=$\frac{1}{2}$OP=$\frac{3}{2}$��OE=$\frac{1}{2}$OB=2��
��Q��$\frac{3}{2}$��2����
��OQ=$\frac{5}{2}$��
����QΪԲ�ģ���OQΪ�뾶�ġ�O�ķ���Ϊ��x-$\frac{3}{2}$��2+��y-2��2=$\frac{25}{4}$��
���� ������Բ���ۺ��⣬��Ҫ�������¶��壬Բ�����ʣ�������Ǻ����������ε���λ�߶������Ȿ��Ĺؼ��������B�����꣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
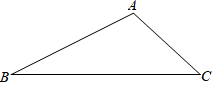 ��ͼ����֪��ABC�����ó߹���ͼ����BC����һ��M��ʹ��AM+MC=BC��������ͼ�ۼ�����д��������
��ͼ����֪��ABC�����ó߹���ͼ����BC����һ��M��ʹ��AM+MC=BC��������ͼ�ۼ�����д���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
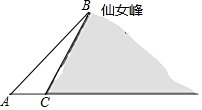 ��ѧ���ۺ���ʵ�������У���ʦ����ͬѧ������¦���н�����������ͼ��ʾ����Ů��ĸ߶ȣ����ʢͬѧ������ѧ����ѧ֪ʶ�����һ��ʵ����������ʵʩ�����²���������ˮƽ����A�����ɽ��B�����ǡ�BACΪ38.7�㣬����A��ˮƽ����ǰ��377����ɽ��C�������ɽ��BC���¶�Ϊ1��0.6�����������Ů��ĸ߶ȣ��ο����ݣ�tan38.7���0.8��
��ѧ���ۺ���ʵ�������У���ʦ����ͬѧ������¦���н�����������ͼ��ʾ����Ů��ĸ߶ȣ����ʢͬѧ������ѧ����ѧ֪ʶ�����һ��ʵ����������ʵʩ�����²���������ˮƽ����A�����ɽ��B�����ǡ�BACΪ38.7�㣬����A��ˮƽ����ǰ��377����ɽ��C�������ɽ��BC���¶�Ϊ1��0.6�����������Ů��ĸ߶ȣ��ο����ݣ�tan38.7���0.8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
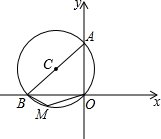 ��ͼ����C��ԭ�㣬������������ֱ��ڵ�A����B����A������Ϊ��0��4����M�ǵ���������$\widehat{OB}$��һ�㣬��BMO=120�㣬���C�İ뾶��Ϊ��������
��ͼ����C��ԭ�㣬������������ֱ��ڵ�A����B����A������Ϊ��0��4����M�ǵ���������$\widehat{OB}$��һ�㣬��BMO=120�㣬���C�İ뾶��Ϊ��������| A�� | 5 | B�� | 4 | C�� | 3 | D�� | 4$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com