
分析 列表得出所有等可能的情况数,找出在二次函数y=(x-m)2+n的顶点在坐标轴上的情况数,即可求出所求的概率.
解答 解:列表如下:
| 0 | -1 | 2 | 1 | |
| -2 | (0,-2) | (-1,-2) | (2,-2) | (1,-2) |
| 0 | (0,0) | (-1,0) | (2,0) | (1,0) |
| 3 | (0,3) | (-1,3) | (2,3) | (1,3) |
点评 此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:选择题
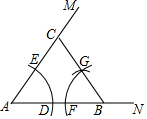 如图,已知∠MAN=55°,点B为AN上一点.用尺规按如下过程作图:
如图,已知∠MAN=55°,点B为AN上一点.用尺规按如下过程作图:| A. | 70° | B. | 110° | C. | 125° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示:
商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,三角形三个顶点坐标分别为O(0,0),A(2,0),B(1,2).若O,B两点的位置不变,点M在x轴上,则点M在什么位置时,三角形OMB的面积是三角形OAB面积的2倍?(即求出点M的坐标)
如图,三角形三个顶点坐标分别为O(0,0),A(2,0),B(1,2).若O,B两点的位置不变,点M在x轴上,则点M在什么位置时,三角形OMB的面积是三角形OAB面积的2倍?(即求出点M的坐标)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com