
【题目】小明和小亮两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
![]() 请计算“
请计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
![]() 一位同学说:“根据实验,一次实验中出现
一位同学说:“根据实验,一次实验中出现![]() 点朝上的概率最大”.这位同学的说法正确吗?为什么?
点朝上的概率最大”.这位同学的说法正确吗?为什么?
![]() 小明和小亮各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为
小明和小亮各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为![]() 的倍数的概率.
的倍数的概率.
【答案】![]() “
“![]() 点朝上”的频率为
点朝上”的频率为![]() ,“
,“![]() 点朝上”的频率为
点朝上”的频率为![]() .
.![]() 不正确,理由见解析;(3)两枚骰子朝上的点数之和为
不正确,理由见解析;(3)两枚骰子朝上的点数之和为![]() 的倍数的概率是
的倍数的概率是![]() .
.
【解析】
(1)由共做了60次实验,“3点朝上”和“5点朝上”的次数分别为6,20,即可求得“3点朝上”的频率和“5点朝上”的频率.
(2)由一次实验中的频率不能等于概率,可得这位同学的说法不正确;
(3)首先根据题意列出表格,然后由表格求得所有等可能的结果与两枚骰子朝上的点数之和为3的倍数的情况,再利用概率公式即可求得答案.
![]() ∵共做了
∵共做了![]() 次实验,“
次实验,“![]() 点朝上”和“
点朝上”和“![]() 点朝上”的次数分别为
点朝上”的次数分别为![]() ,
,![]() ,
,
∴“![]() 点朝上”的频率为:
点朝上”的频率为:![]() ,“
,“![]() 点朝上”的频率为
点朝上”的频率为![]() .
.
![]() 不正确,
不正确,
∵一次实验中的频率不能等于概率,
∴不正确;
![]() 列表得:
列表得:
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∵一共有![]() 种情况,两枚骰子朝上的点数之和为
种情况,两枚骰子朝上的点数之和为![]() 的倍数的有
的倍数的有![]() 种情况;
种情况;
∴两枚骰子朝上的点数之和为![]() 的倍数的概率是:
的倍数的概率是:![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】某果园有![]() 棵枇杷树.每棵平均产量为
棵枇杷树.每棵平均产量为![]() 千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量
千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量![]() 千克,若设增种
千克,若设增种![]() 棵枇杷树,投产后果园枇杷的总产量为
棵枇杷树,投产后果园枇杷的总产量为![]() 千克,则
千克,则![]() 与
与![]() 之间的函数关系式为________.
之间的函数关系式为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面每个语句中,都给出了两件可能发生的事情,其中发生的机会相同的是( )
A. 两次掷骰子,掷出的数的和大于![]() 与掷出的数的和不大于
与掷出的数的和不大于![]()
B. 掷骰子掷出的数是偶数与掷出的数是奇数
C. 最后一节课是数学与最后一节课不是数学
D. 冬天里下雪和夏天里下雪
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在三角形纸片![]() 中,
中,![]() ,
,![]() ,将纸片的一角折叠,使点
,将纸片的一角折叠,使点![]() 落在
落在![]() 内的点
内的点![]() 处.
处.
(1)若![]() ,
,![]() ________.
________.
(2)如图①,若各个角度不确定,试猜想![]() ,
,![]() ,
,![]() 之间的数量关系,直接写出结论.
之间的数量关系,直接写出结论.
②当点![]() 落在四边形
落在四边形![]() 外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,
外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,![]() ,
,![]() ,
,![]() 之间又存在什么关系?请说明。
之间又存在什么关系?请说明。
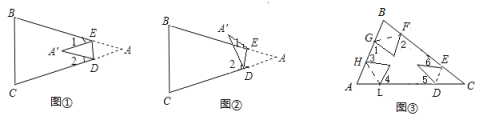
(3)应用:如图③:把一个三角形的三个角向内折叠之后,且三个顶点不重合,那么图中的![]() 和是________.
和是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m,n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0.
∴(m﹣n)2+(n﹣4)2=0,∵(m﹣n)2≥0,(n﹣4)2≥0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)已知:x2+2xy+2y2+2y+1=0,求2x+y的值;
(2)已知:△ABC的三边长a,b,c都是正整数,且满足:a2+b2﹣12a﹣16b+100=0,求△ABC的最大边c的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,动点
,动点![]() 在线段
在线段![]() 和射线
和射线![]() 上运动.
上运动.
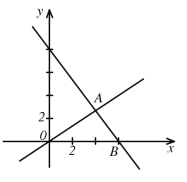
(1)求直线![]() 的函数关系式.
的函数关系式.
(2)求![]() 的面积.
的面积.
(3)是否存在点![]() ,使
,使![]() 的面积与
的面积与![]() 的面积相等?若存在求出此时点
的面积相等?若存在求出此时点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AF、CE分别是∠BAD和∠BCD的角平分线,根据现有的图形,请添加一个条件,使四边形AECF为菱形,则添加的一个条件可以是__________.(只需写出一个即可,图中不能再添加别的“点”和“线”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,E为AB中点,D为AC上一点,BF//AC交DE的延长线长于点F,AC=6,BC=5.则四边形FBCD周长的最小值是( )

A.21B.16C.17D.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com