
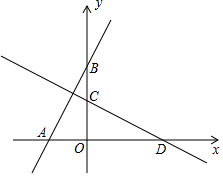
 如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.
如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.分析 (1)依题意求出点B坐标,然后用待定系数法求解析式;
(2)设OB=m,则AD=m+2,根据三角形面积公式得到关于m的方程,解方程求得m的值,然后根据弧长公式即可求得.
解答 解:(1)∵OB=4,
∴B(0,4)
∵A(-2,0),
设直线AB的解析式为y=kx+b,
则$\left\{\begin{array}{l}{-2k+b=0}\\{b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=4}\end{array}\right.$,
∴直线AB的解析式为y=2x+4;
(2)设OB=m,则AD=m+2,
∵△ABD的面积是5,
∴$\frac{1}{2}$AD•OB=5,
∴$\frac{1}{2}$(m+2)•m=5,即m2+2m-10=0,
解得m=-1+$\sqrt{11}$或m=-1-$\sqrt{11}$(舍去),
∵∠BOD=90°,
∴点B的运动路径长为:$\frac{1}{4}$×2π×(-1+$\sqrt{11}$)=$\frac{-1+\sqrt{11}}{2}$π.
点评 本题考查的是待定系数法求一次函数的解析式以及三角形面积公式和弧长计算,难度一般.


科目:初中数学 来源: 题型:解答题
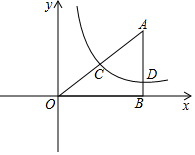 如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=$\frac{3}{5}$.
如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为30°,已知BE=2m,此学生身高CD=1.7m,求大树的高度.(结果保留根号)
数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为30°,已知BE=2m,此学生身高CD=1.7m,求大树的高度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
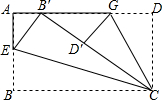 如图,将一张矩形纸片ABCD的边BC斜着向AD边对折,使点B落在AD上,记为B′,折痕为CE;再将CD边斜向下对折,使点D落在B′C边上,记为D′,折痕为CG,B′D′=2,BE=$\frac{1}{3}$BC.则矩形纸片ABCD的面积为15.
如图,将一张矩形纸片ABCD的边BC斜着向AD边对折,使点B落在AD上,记为B′,折痕为CE;再将CD边斜向下对折,使点D落在B′C边上,记为D′,折痕为CG,B′D′=2,BE=$\frac{1}{3}$BC.则矩形纸片ABCD的面积为15.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24π | B. | 21π | C. | 16.8π | D. | 36π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
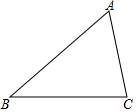 如图,△ABC中,∠ACB>∠ABC.
如图,△ABC中,∠ACB>∠ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com