
 如图,以1为腰长画等腰直角三角形Rt△ACB,又以Rt△ACB的斜边AC长为直角边画第2个等腰直角三角形Rt△ADC,再以Rt△ADC的斜边AD长为直角边画第3个等腰直角三角形Rt△ADE,依此类推,则第2015个等腰直角三角形的斜边长为${(\sqrt{2})}^{2015}$.
如图,以1为腰长画等腰直角三角形Rt△ACB,又以Rt△ACB的斜边AC长为直角边画第2个等腰直角三角形Rt△ADC,再以Rt△ADC的斜边AD长为直角边画第3个等腰直角三角形Rt△ADE,依此类推,则第2015个等腰直角三角形的斜边长为${(\sqrt{2})}^{2015}$. 分析 根据等腰直角三角形的斜边长为直角边长度的$\sqrt{2}$倍,可以发现n个△,直角边是第(n-1)个△的斜边长,即可求出斜边长.
解答 解:等腰直角三角形一个直角边为1,
等腰直角三角形的斜边长为直角边长度的$\sqrt{2}$倍,
第一个△的斜边长:1×$\sqrt{2}$=$\sqrt{2}$,
第二个△直角边是第一个△的斜边长,所以它的斜边长:$\sqrt{2}×\sqrt{2}$=${(\sqrt{2})}^{2}$,
…
第n个△,直角边是第(n-1)个△的斜边长,其斜边长为:${(\sqrt{2})}^{n}$,
则第2015个等腰直角三角形的斜边长是:${(\sqrt{2})}^{2015}$.
故答案为:${(\sqrt{2})}^{2015}$.
点评 此题主要考查学生对等腰直角三角形的理解和掌握,解答此题的关键是通过认真分析,根据等腰直角三角形的斜边长为直角边长度的$\sqrt{2}$倍,从中发现规律.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
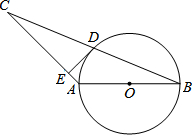 如图,△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E.
如图,△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=ax2+bx-8(a≠0)经过A(-2,0),B(4,0)两点,与y轴交于点C.
已知抛物线y=ax2+bx-8(a≠0)经过A(-2,0),B(4,0)两点,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 1 | 2 | 8 | 13 | 14 | 4 |
| A. | 70,80 | B. | 70,90 | C. | 80,90 | D. | 90,100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com