
 如图,∠ABD,∠ACD的10等分线相交于点G1,G2…G9,若∠BDC=140°,∠BG1C=∠77°,求∠A的度数.
如图,∠ABD,∠ACD的10等分线相交于点G1,G2…G9,若∠BDC=140°,∠BG1C=∠77°,求∠A的度数. 分析 由角平分线的性质可得:∠BDC=∠A+∠ABD+∠ACD,∠BG1C=∠A+∠ABG1+∠ACG1,而∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,则∠ABG1=$\frac{1}{10}$∠ABD,∠ACG1=$\frac{1}{10}$∠ACD,所以10∠BG1C=10∠A+∠ABD+∠ACD,利用等式的性质得到10∠BG1C-∠BDC=9∠A,进而可求出∠A的度数.
解答 解:∵∠BDC=∠A+∠ABD+∠ACD,∠BG1C=∠A+∠ABG1+∠ACG1,
而∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,
∴∠ABG1=$\frac{1}{10}$∠ABD,∠ACG1=$\frac{1}{10}$∠ACD,
∴10∠BG1C=10∠A+∠ABD+∠ACD,
∴10∠BG1C-∠BDC=9∠A,
∴∠A=$\frac{1}{9}$(10×77°-140°)=70°.
点评 此题考查了三角形内角和定理和三角形的外角的性质,要熟练掌握,解答此题的关键是要明确:三角形的外角等于和它不相邻的两个内角的和.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:解答题
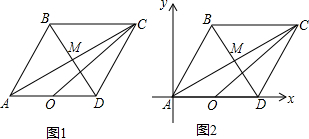
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
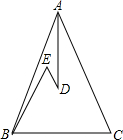 如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=9cm,DE=3cm,则BC=12cm.
如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=9cm,DE=3cm,则BC=12cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种树 | 乙种树 | 丙种树 | 总数 | |
| 三种树的棵树 | 2x | x | y | 20 |
| 三种树的金额 | 400x | 300x | 500y | 6800 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
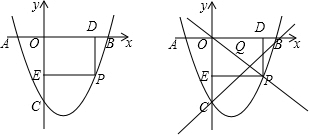
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
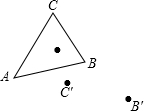 如图所示,小明在黑板上画△ABC绕一点P旋转45°角的旋转图时,当他完成B,C两点分别旋转到点B′,C′时,不小心把旋转中心擦掉了,没有了旋转中心,小明不知道如何画下去,你能帮助他画完图形吗?
如图所示,小明在黑板上画△ABC绕一点P旋转45°角的旋转图时,当他完成B,C两点分别旋转到点B′,C′时,不小心把旋转中心擦掉了,没有了旋转中心,小明不知道如何画下去,你能帮助他画完图形吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
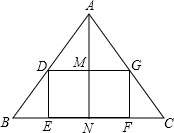 如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,SDEFG=y.
如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,SDEFG=y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com