
| A. | 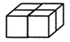 | B. |  | C. | 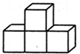 | D. | 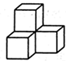 |
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校数学兴趣小组在探究如何求tan 15°,cos15°的值,经过自主思考、合作交流讨论,得到以下思路:
某校数学兴趣小组在探究如何求tan 15°,cos15°的值,经过自主思考、合作交流讨论,得到以下思路:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
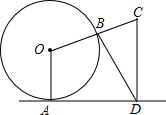 如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=70度.
如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=70度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
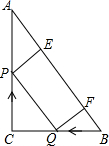 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,动点P,Q分别从点C,B开始沿边CA,BC匀速运动,点Q的速度为1cm/s,运动时间为ts.过点P作PE⊥AB,过点Q作QF⊥AB,垂足分别为E,F.
如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,动点P,Q分别从点C,B开始沿边CA,BC匀速运动,点Q的速度为1cm/s,运动时间为ts.过点P作PE⊥AB,过点Q作QF⊥AB,垂足分别为E,F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两边相等的平行四边形是菱形 | |
| B. | 有一个角是直角的四边形是矩形 | |
| C. | 四个角相等的菱形是正方形 | |
| D. | 两条对角线互相垂直且相等的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形AOCB在平面直角坐标系x0y中,点O为原点,点B在反比例函数y=$\frac{16}{x}$(x>0)图象上.
如图,正方形AOCB在平面直角坐标系x0y中,点O为原点,点B在反比例函数y=$\frac{16}{x}$(x>0)图象上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≤2 | B. | a>2 | C. | a>3 | D. | a≥3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧$\widehat{MN}$的长为$\frac{6}{5}$π,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B.
如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧$\widehat{MN}$的长为$\frac{6}{5}$π,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com