
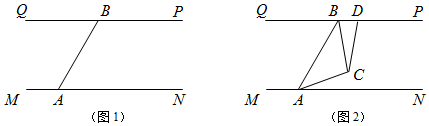
分析 (1)根据∠BAM+∠BAN=180°,∠BAM:∠BAN=2:1,即可得到∠BAN的度数;
(2)设A灯转动t秒,两灯的光束互相平行,分两种情况进行讨论:当0<t<90时,根据2t=1•(30+t),可得 t=30;当90<t<150时,根据1•(30+t)+(2t-180)=180,可得t=110;
(3)设灯A射线转动时间为t秒,根据∠BAC=2t-120°,∠BCD=120°-∠BCD=t-60°,即可得出∠BAC:∠BCD=2:1,据此可得∠BAC和∠BCD关系不会变化.
解答 解:(1)∵∠BAM+∠BAN=180°,∠BAM:∠BAN=2:1,
∴∠BAN=180°×$\frac{1}{3}$=60°,
故答案为:60;
(2)设A灯转动t秒,两灯的光束互相平行,
①当0<t<90时,如图1,
∵PQ∥MN,
∴∠PBD=∠BDA,
∵AC∥BD,
∴∠CAM=∠BDA,
∴∠CAM=∠PBD
∴2t=1•(30+t),
解得 t=30;
②当90<t<150时,如图2,
∵PQ∥MN,
∴∠PBD+∠BDA=180°,
∵AC∥BD,
∴∠CAN=∠BDA
∴∠PBD+∠CAN=180°
∴1•(30+t)+(2t-180)=180,
解得 t=110,
综上所述,当t=30秒或110秒时,两灯的光束互相平行;
(3)∠BAC和∠BCD关系不会变化.
理由:设灯A射线转动时间为t秒,
∵∠CAN=180°-2t,
∴∠BAC=60°-(180°-2t)=2t-120°,
又∵∠ABC=120°-t,
∴∠BCA=180°-∠ABC-∠BAC=180°-t,而∠ACD=120°,
∴∠BCD=120°-∠BCD=120°-(180°-t)=t-60°,
∴∠BAC:∠BCD=2:1,
即∠BAC=2∠BCD,
∴∠BAC和∠BCD关系不会变化.
点评 本题主要考查了平行线的性质以及角的和差关系的运用,解决问题的关键是运用分类思想进行求解,解题时注意:两直线平行,内错角相等;两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:解答题
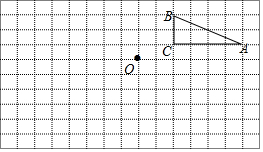 如图,在边长为1个单位长度的小正方形组成的网格中,点A,B,C,O都在格点上.
如图,在边长为1个单位长度的小正方形组成的网格中,点A,B,C,O都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
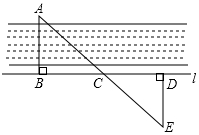 如图,要测量河两岸相对两点A、B间的距高,先在过点B的AB的垂线上取两点C、D,使得CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可以证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC的理由是( )
如图,要测量河两岸相对两点A、B间的距高,先在过点B的AB的垂线上取两点C、D,使得CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可以证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC的理由是( )| A. | SAS | B. | SSS | C. | ASA | D. | AAS |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
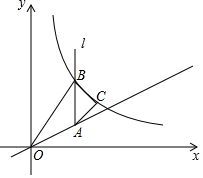 如图,已知点A是一次函数y=$\frac{1}{2}$x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=$\frac{k}{x}$(x>0)的图象过点B,C,若△OAB的面积为6,则△ABC的面积是3.
如图,已知点A是一次函数y=$\frac{1}{2}$x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=$\frac{k}{x}$(x>0)的图象过点B,C,若△OAB的面积为6,则△ABC的面积是3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com