
���� ��1����2������ͼ�ο�ֱ�ӵĵó����ۣ�
��3�������B���ʾ������Ȼ���������������ľ��빫ʽ�������ľ�������������ʾ������ľ���ֵ�����㼴�ɣ�
��� �⣺��1����ͼ��֪����A��ʾ��-3������A�����ƶ�7����λ���ȣ���ô�յ�B��ʾ������4��A��B�����ľ�����|-3-4|=7��
��2�������A��ʾ��3������A�����ƶ�57��λ���ȣ����A��ʾ3-7=-4���������ƶ�5����λ���ȣ���ô�յ�B��ʾ������-4+5=1��A��B�����ľ�����|3-1|=2��
�ʴ�Ϊ��1��2��
��3����A��ʾ��Ϊa������A�����ƶ�b����λ���ȣ����A��ʾa+b���������ƶ�c����λ���ȣ���ô�յ�B��ʾ������a+b-c��A��B�����ľ�����|a+b-c-a|=|b-c|��
�ʴ�Ϊ��4��7��1��2��a+b-c��|b-c|��
���� ���⿼��������ᣬ��֪�����ϵ���ƶ����ɺ������ľ��빫ʽ�ǽ�����Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
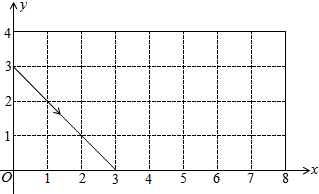 ��ͼ������P�ӣ�0��3������������ͼ��ʾ�ķ����˶���ÿ���������εı�ʱ����������ʱ����ǵ�������ǣ�����P��2015���������εı�ʱ����P������Ϊ��1��4����
��ͼ������P�ӣ�0��3������������ͼ��ʾ�ķ����˶���ÿ���������εı�ʱ����������ʱ����ǵ�������ǣ�����P��2015���������εı�ʱ����P������Ϊ��1��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 4 | C�� | 3 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
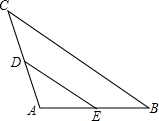 ��ͼ���ڡ�ABC�У���A=110�㣬DE��CB������CDE=140�㣬���B�Ķ���Ϊ��������
��ͼ���ڡ�ABC�У���A=110�㣬DE��CB������CDE=140�㣬���B�Ķ���Ϊ��������| A�� | 20�� | B�� | 30�� | C�� | 35�� | D�� | 40�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com