

分析 问题1:根据三角形的外角的性质即可得到结论;
问题2:根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;
解决问题1:根据四边形的内角和等于360°可得(180°-∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°-∠3)+∠D=360°,然后整理即可得解;
解决问题2:根据(1)的结论∠B+∠BAD=∠D+∠BCD,∠PAD+∠P=∠D+∠PCD,然后整理即可得解.
解答  解:问题1:连接PO并延长.
解:问题1:连接PO并延长.
则∠1=∠A+∠2,∠3=∠C+∠4,
∵∠2+∠4=∠P,∠1+∠3=∠AOC,
∴∠AOC=∠A+∠C+∠P;
故答案为:∠AOC=∠A+∠C+∠P;
问题2:如图2,∵AP、CP分别平分∠BAD、∠BCD,
∴∠1=∠2,∠3=∠4,
∵∠2+∠B=∠3+∠P,
∠1+∠P=∠4+∠D,
∴2∠P=∠B+∠D,
∴∠P=$\frac{1}{2}$(∠B+∠D)=$\frac{1}{2}$×(28°+48°)=38°;
解决问题1:如图3,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴(180°-2∠1)+∠B=(180°-2∠4)+∠D,
在四边形APCB中,(180°-∠1)+∠P+∠4+∠B=360°,
在四边形APCD中,∠2+∠P+(180°-∠3)+∠D=360°,
∴2∠P+∠B+∠D=360°,
∴∠P=180°-$\frac{1}{2}$(∠B+∠D);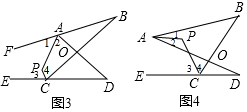
解决问题2:如图4,∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∵(∠1+∠2)+∠B=(180°-2∠3)+∠D,
∠2+∠P=(180°-∠3)+∠D,
∴2∠P=180°+∠D+∠B,
∴∠P=90°+$\frac{1}{2}$(∠B+∠D).
故答案为:∠P=90°+$\frac{1}{2}$(∠B+∠D).
点评 本题考查了三角形的内角和定理,角平分线的定义,准确识图并运用好“8字形”的结论,然后列出两个等式是解题的关键,用阿拉伯数字加弧线表示角更形象直观.


科目:初中数学 来源: 题型:解答题
 (1)计算:|-2+$\sqrt{3}$|+(-1)2017-(π+1)0+$\sqrt{3}$;
(1)计算:|-2+$\sqrt{3}$|+(-1)2017-(π+1)0+$\sqrt{3}$;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A,B,C分别是⊙O上的点,且∠B=60°,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
如图,点A,B,C分别是⊙O上的点,且∠B=60°,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次提现 | 第二次提现 | 第三次提现 | |
| 提现金额(元) | a | b | a+2b |
| 手续费(元) | 0 | 0.3 | 1.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com