
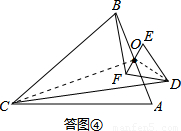
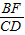 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)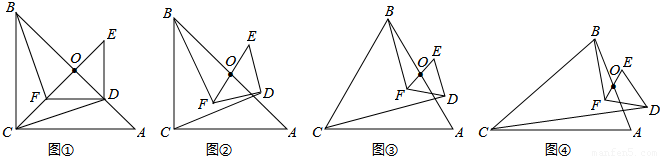
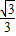 ;
;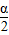 .
.
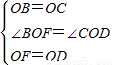

 =tan30°=
=tan30°=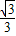 ,∠BOC=90°.
,∠BOC=90°.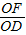 =tan30°=
=tan30°=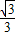 ,∠DOF=90°.
,∠DOF=90°.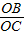 =
=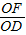 =
=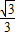 .
.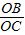 =
=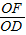 =
=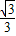 ,∠BOF=∠COD,
,∠BOF=∠COD,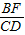 =
= .
.
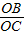 =tan
=tan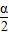 ,∠BOC=90°.
,∠BOC=90°.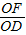 =tan
=tan ,∠DOF=90°.
,∠DOF=90°.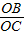 =
=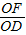 =tan
=tan .
.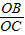 =
=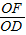 =tan
=tan ,∠BOF=∠COD,
,∠BOF=∠COD,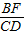 =tan
=tan .
.

科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| BF | CD |

查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁鞍山第26中学九年级上学期第三次月考数学试卷(解析版) 题型:解答题
阅读材料

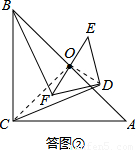
如图①,△ABC与△DEF都是等腰直角三角形,ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.解决问题:
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)
查看答案和解析>>
科目:初中数学 来源:2012年苏教版初中数学七年级下 11.2全等三角形练习卷(解析版) 题型:解答题
阅读下列材料:
如图(1)所示,把△ABC沿直线BC移动线段BC那样长的距离可以变到△ECD的位置;
如图(2)所示,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;
如图(3)所示,以点A为中心,把△ABC旋转180°,可以变到△AED的位置.
像这样,只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换. 在全等变换中可以清楚地识别全等三角形的对应元素,以上的三种全等变换分别叫平移变换、翻折变换和旋转变换.
问题:如图(4),△ABC≌△DEF,B和E、C和F是对应顶点,问通过怎样的全等变换可以使它们重合,并指出它们相等的边和角.
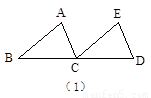
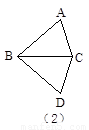
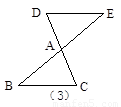
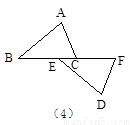
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com