
【题目】如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2与y轴交于点C(0,4),其中x1,x2是方程x2﹣4x﹣12=0的两个根.
(1)求抛物线的解析式;
(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连结CM,当△CMN的面积最大时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的点F的坐标;若不存在,请说明理由.

【答案】(1)抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣4;(2)点M的坐标为(2,0);(3)F1(﹣6,0),F2(2,0),F3(8﹣2
x﹣4;(2)点M的坐标为(2,0);(3)F1(﹣6,0),F2(2,0),F3(8﹣2![]() ,0),F4(8+2
,0),F4(8+2![]() ,0).
,0).
【解析】试题分析:(1)根据一元二次方程解法得出A,B两点的坐标,再利用交点式求出二次函数解析式;
(2)首先判定△MNA∽△BCA.得出![]() ,进而得出函数的最值;
,进而得出函数的最值;
(3)分别根据当AF为平行四边形的边时,AF平行且等于DE与当AF为平行四边形的对角线时,分析得出符合要求的答案.
试题解析:(1)∵x2﹣4x﹣12=0,
∴x1=﹣2,x2=6.
∴A(﹣2,0),B(6,0),
又∵抛物线过点A、B、C,故设抛物线的解析式为y=a(x+2)(x﹣6),
将点C的坐标代入,求得a=![]() ,
,
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣4;
x﹣4;
(2)设点M的坐标为(m,0),过点N作NH⊥x轴于点H(如图(1)).
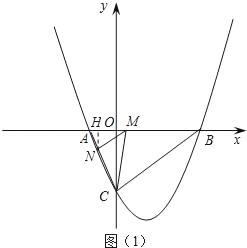
∵点A的坐标为(﹣2,0),点B的坐标为(6,0),
∴AB=8,AM=m+2,
∵MN∥BC,
∴△MNA∽△BCA.
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴NH=![]() ,
,
∴S△CMN=S△ACM﹣S△AMN=![]() AMCO﹣
AMCO﹣![]() AMNH,
AMNH,
=![]() m+2)(4﹣
m+2)(4﹣![]() )=﹣
)=﹣![]() m2+m+3,
m2+m+3,
=﹣![]() (m﹣2)2+4.
(m﹣2)2+4.
∴当m=2时,S△CMN有最大值4.
此时,点M的坐标为(2,0);
(3)∵点D(4,k)在抛物线y=![]() x2﹣
x2﹣![]() x﹣4上,
x﹣4上,
∴当x=4时,k=﹣4,
∴点D的坐标是(4,﹣4).
①如图(2),当AF为平行四边形的边时,AF平行且等于DE,
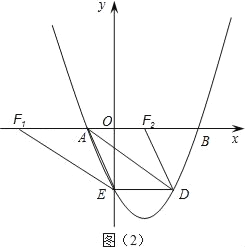
∵D(4,﹣4),
∴DE=4.
∴F1(﹣6,0),F2(2,0),
②如图(3),当AF为平行四边形的对角线时,设F(n,0),
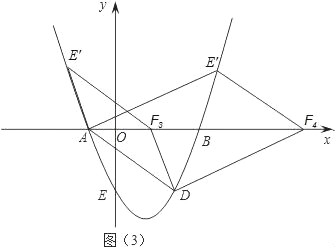
∵点A的坐标为(﹣2,0),
则平行四边形的对称中心的横坐标为:![]() ,
,
∴平行四边形的对称中心坐标为(![]() ,0),
,0),
∵D(4,﹣4),
∴E'的横坐标为:![]() ﹣4+
﹣4+![]() =n﹣6,
=n﹣6,
E'的纵坐标为:4,
∴E'的坐标为(n﹣6,4).
把E'(n﹣6,4)代入y=![]() x2﹣
x2﹣![]() x﹣4,得n2﹣16n+36=0.
x﹣4,得n2﹣16n+36=0.
解得n=8±2![]() .F3(8﹣2
.F3(8﹣2![]() ,0),F4(8+2
,0),F4(8+2![]() ,0),
,0),
综上所述F1(﹣6,0),F2(2,0),F3(8﹣2![]() ,0),F4(8+2
,0),F4(8+2![]() ,0).
,0).


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】铜仁某校高中一年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次.甲、乙两名同学测试情况如图所示:

![]() 根据图6提供的信息填写下表:
根据图6提供的信息填写下表:
平均数 | 众数 | 方差 | |
甲 |
| ||
乙 |
|
![]() 如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
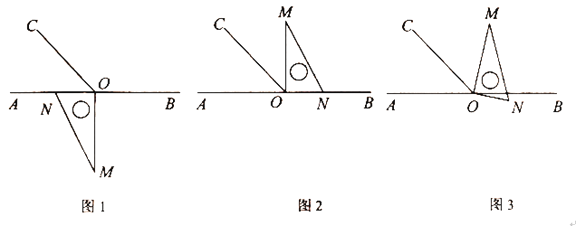
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使![]() ,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为______度;
(2)在(1)旋转过程中,当旋转至图3的位置时,使得OM在∠BOC的内部,ON落在直线AB下方,试探究∠COM与∠BON之间满足什么等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中正确的有( )
①经过一点,有且只有一条直线与已知直线平行;②有公共顶点且和为![]() 的两个角是邻补角;③两条直线被第三条直线所截,同旁内角互补;④不相交的两条直线叫做平行线;⑤直线外的一点到已知直线的垂线段叫做点到直线的距离;
的两个角是邻补角;③两条直线被第三条直线所截,同旁内角互补;④不相交的两条直线叫做平行线;⑤直线外的一点到已知直线的垂线段叫做点到直线的距离;
A.0个;B.1个;C.2个;D.3个;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BE∥AO,![]()
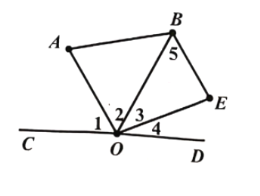
解:因为BE∥AO.(已知)
所以![]()
因为![]() ,(已知 )
,(已知 )
所以 .(等量代换)
![]()
![]()
![]()
![]() .(等式性质)
.(等式性质)
因为 ,(已求)
所以 .(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠BDC=∠EFD,∠AED=∠ACB.
(1)试判断∠DEF与∠B的大小关系,并说明理由;
(2)若D、E、F分别是AB、AC、CD边上的中点,S△DEF=4,求S△ABC.
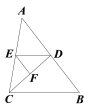
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过对角线BD的中点O作直线EF,分别交DA的延长线,AB, DC,BC的延长线于点E,M,N,F.
(1)求证:△ODE≌△OBF;
(2)除(1)中这对全等三角形外,再写出两对全等三角形(不需要证明).
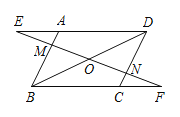
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,![]() ,BD平分∠ABC,BC上有动点P.
,BD平分∠ABC,BC上有动点P.
(1)DP⊥BC时(如图1),求证:![]() ;
;
(2)DP平分∠BDC时(如图2),BD、CD、CP三者有何数量关系?
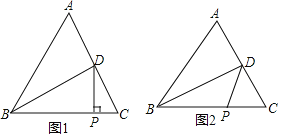
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料1:一般地,![]() 个相同因数
个相同因数![]() 相乘:
相乘:![]() 记为
记为![]() .如
.如![]() ,此时,3叫做以2为底的8的对数,记为
,此时,3叫做以2为底的8的对数,记为![]() (即
(即![]() )
)
(1)计算![]() __________,
__________,![]() __________.
__________.
材料2:新规定一种运算法则:自然数1到![]() 的连乘积用
的连乘积用![]() 表示,例如:
表示,例如:![]() ,
,![]() ,
,![]() ,
,![]() ,…在这种规定下
,…在这种规定下
(2)求出满足该等式的![]() :
:![]()
(3)当![]() 为何值时,
为何值时,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com