
已知:如图,抛物线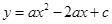 (
(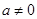 )与
)与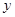 轴交于点
轴交于点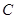 ( 0,4) ,与
( 0,4) ,与 轴交于点
轴交于点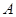 ,
,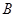 ,点
,点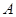 的坐标为(4,0).
的坐标为(4,0).
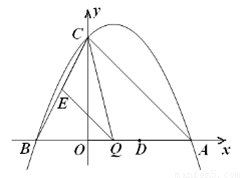
(1) 求该抛物线的解析式;
(2) 点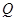 是线段
是线段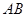 上的动点,过点
上的动点,过点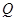 作
作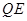 ∥
∥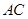 ,交
,交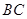 于点
于点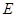 ,连接
,连接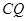 . 当
. 当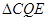 的面积最大时,求点
的面积最大时,求点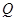 的坐标;
的坐标;
(3)若平行于 轴的动直线与该抛物线交于点
轴的动直线与该抛物线交于点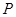 ,与直线
,与直线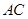 交于点
交于点 ,点
,点 的坐标为(2,0). 问: 是否存在这样的直线,使得
的坐标为(2,0). 问: 是否存在这样的直线,使得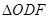 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点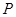 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(1) ;(2)(1,0);(3)(
;(2)(1,0);(3)(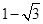 ,3)或(
,3)或(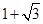 ,3)或(
,3)或(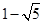 ,2)或(
,2)或( ,2)
,2)
【解析】
试题分析:(1)由抛物线与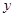 轴交于点
轴交于点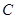 (0,4),与
(0,4),与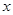 轴交于点
轴交于点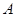 (4,0)根据待定系数法即可求得结果;
(4,0)根据待定系数法即可求得结果;
(2)先求得抛物线与x轴的交点坐标,根据勾股定理可得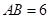 ,
,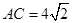 ,
, ,设
,设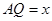 ,
,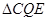 的面积用
的面积用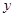 表示,由
表示,由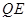 ∥
∥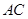 可得
可得 , 即
, 即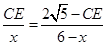 ,即可表示出CE的长,过点
,即可表示出CE的长,过点 作
作 ,垂足为
,垂足为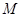 ,在Rt
,在Rt 中求得∠B的正弦函数,在Rt
中求得∠B的正弦函数,在Rt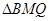 中即可表示出QM的长,从而可以表示出y关于x的函数关系式,再根据二次函数的性质即可求得结果;
中即可表示出QM的长,从而可以表示出y关于x的函数关系式,再根据二次函数的性质即可求得结果;
(3)分 为底边、
为底边、 为腰且
为腰且 为顶角、
为顶角、 为腰且
为腰且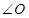 为顶角三种情况分析即可.
为顶角三种情况分析即可.
(1)∵抛物线 (
(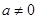 )与
)与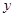 轴交于点
轴交于点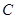 (0,4),与
(0,4),与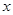 轴交于点
轴交于点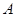 (4,0)
(4,0)
∴ ,解得
,解得 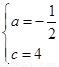
∴该抛物线的解析式为 ;
;
(2)令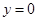 ,则
,则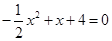 ,解得
,解得 ,
,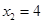
∴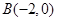
∴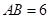 ,
,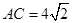 ,
,
设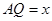 ,
,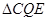 的面积用
的面积用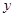 表示,
表示,
∵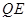 ∥
∥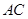
∴ ,即
,即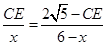
∴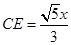
过点 作
作 ,垂足为
,垂足为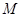

在Rt 中,
中,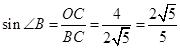
在Rt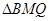 中,
中,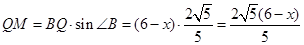
∴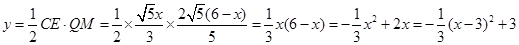
∴当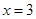 时,
时,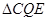 的面积最大是3,即点
的面积最大是3,即点 的坐标为(1,0);
的坐标为(1,0);
(3)①当 为底边时,点
为底边时,点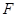 的横坐标是1,又点
的横坐标是1,又点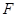 在直线
在直线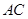 上,直线
上,直线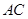 的解析式为
的解析式为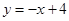 ,所以点
,所以点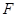 的坐标是(1,3),所以点
的坐标是(1,3),所以点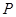 的纵坐标为3,代入
的纵坐标为3,代入 ,得点
,得点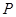 的坐标为(
的坐标为(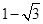 ,3)或(
,3)或(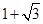 ,3)
,3)
②当 为腰,
为腰, 为顶角时,此时点
为顶角时,此时点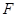 是以点
是以点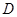 为圆心,
为圆心,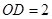 为半径的圆与直线
为半径的圆与直线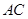 的交点,有两个点,点
的交点,有两个点,点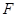 (4,0)与点
(4,0)与点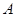 重合,舍去,点
重合,舍去,点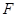 (2,2),所以点
(2,2),所以点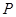 的纵坐标为2,,代入
的纵坐标为2,,代入 ,得点
,得点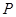 的坐标为(
的坐标为(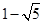 ,2)或(
,2)或( ,2)
,2)
③当 为腰,
为腰,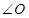 为顶角时,此时点
为顶角时,此时点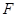 应是以点
应是以点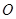 为圆心,
为圆心,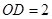 为半径的圆与直线
为半径的圆与直线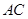 的交点,但是点
的交点,但是点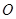 到
到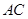 的距离为
的距离为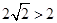 ,所以不存在满足条件的点
,所以不存在满足条件的点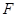 .
.
考点:二次函数的综合题
点评:本题知识点较多,综合性强,难度较大,一般是中考压轴题,需要学生熟练掌握二次函数的性质的应用.


科目:初中数学 来源: 题型:
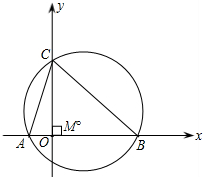 与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.
与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.查看答案和解析>>
科目:初中数学 来源: 题型:
 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12,查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(1-
(2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(1-| 3 |
| ||
| 2 |
| 5 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).
已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.
已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com