练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    我们知道：正方形，正六边形可以密铺，而正十二边形是不能密铺的．试问：用边长相等的正方形、正六边形、正十二边形的组合能否密铺？如果可以，请设计出一个可以密铺的图案来；如果仍然不行，请说明理由．

    答案：能
    解析：

    解：由于正方形，正六边形，正十二边形的每个内角分别为90°，120°和150°，而90°＋120°＋150°＝360°，故而可知它们的组合是可以密铺的．

    由正方形，正六边形，正十二边形的组合可以密铺．事实上，在每个拼接点处，只要依次用一个正方形、一个正六边形和一个正十二边形，它们一定可以拼成无缝隙且没有重叠的图案来．如图所示即是由它们的组合所拼成的一个图案．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

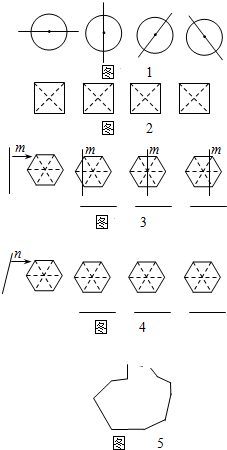    （2013•池州一模）我们知道：由于圆是中心对称图形，所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分（如图1）．
    探索下列问题：
    （1）在如图2给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分；
    （2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2．
    ①请你在如图3中相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）；
    ②请你在如图4中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）．
    （3）是否存在一条直线，将一个任意的平面图形（如图5）分割成面积相等的两部分？请简略说出理由．

    查看答案和解析>>

    科目：初中数学 来源：新课标读想练　七年级数学(下) 人教版 题型：044

    我们知道：正方形、正六边形可以密铺，而正十二边形是不能密铺的．试问：用边长相等的正方形、正六边形、正十二边形的组合能否密铺？如果可以，请设计出一个可以密铺的图案来；如果仍然不行，请说明理由．

    查看答案和解析>>

    同步练习册答案