
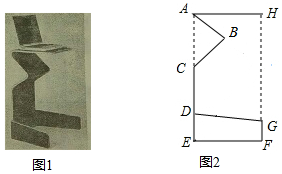
 如图1是一张创意电脑桌,图2是其平面示意图,已知以A、E、F、H为顶点的四边形,点C、D在AE上,点G在HF上,测得AC=CD=2DE,DE=$\frac{4}{3}$GF,AB=CB=31.2cm,AH=50cm,∠BAH=40°.
如图1是一张创意电脑桌,图2是其平面示意图,已知以A、E、F、H为顶点的四边形,点C、D在AE上,点G在HF上,测得AC=CD=2DE,DE=$\frac{4}{3}$GF,AB=CB=31.2cm,AH=50cm,∠BAH=40°.分析 (1)根据锐角三角函数和题目中的数据可以去的GH的长;
(2)根据(1)中的答案,作出合适的辅助线,可以求得tan∠EDG的值.
解答 解:(1)∵AB=CB=31.2cm,∠BAH=40°,∠HAC=90°,cos50°=0.642,
∴∠BAC=50°,
∴AC=2AB•cos∠BAC=2×31.2×0.642≈40.1cm,
∵AC=CD=2DE,DE=$\frac{4}{3}$GF,AE=HF,
∴AE=AC+CD+DE=40.1+40.1+(40.1÷2)≈100.3cm,
∴HF=100.3cm,GF=$\frac{3}{4}(40.1÷2)$≈15.0cm,
∴GH=HF-GF=100.3-15.0=85.3cm,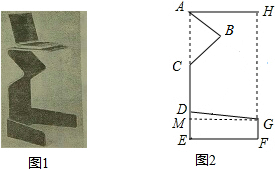
即GH的长是85.3cm;
(2)作GM⊥DE于点M,
∵AH=50cm,GF=15cm,DE=40.1÷2≈20cm,
∴DM=5cm,
∴tan∠EDG=$\frac{GM}{DM}=\frac{50}{5}=10$,
即tan∠EDG=10.
点评 本题考查解直角三角形、等腰三角形的性质、锐角三角函数,解答本题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数解答.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (m-2)(m+2)=m2-2 | B. | (x-6)(x+6)=x2+36 | C. | (x-y)(x+y)=x2-y2 | D. | (x+y)(x+y)=x2+y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 14×104 | B. | 1.4×102 | C. | 14×105 | D. | 1.4×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-l,2) | C. | (-2,-1) | D. | (1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
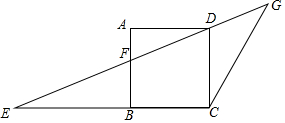 如图,正方形ABCD的边BC恰好在△ECG边EC上,点D在边EG上,AB与EG交于点F.
如图,正方形ABCD的边BC恰好在△ECG边EC上,点D在边EG上,AB与EG交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com