
【题目】如图,在△ABC中,AD平分∠BAC , 按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 ![]() AD的长为半径在AD两侧作弧,交于两点M、N;
AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF .
若BD=6,AF=4,CD=3,则BE的长是( ).
A.2
B.4
C.6
D.8
【答案】D
【解析】:∵根据作法可知:MN是线段AD的垂直平分线,
∴AE=DE , AF=DF ,
∴∠EAD=∠EDA ,
∵AD平分∠BAC ,
∴∠BAD=∠CAD ,
∴∠EDA=∠CAD ,
∴DE∥AC ,
同理DF∥AE ,
∴四边形AEDF是菱形,
∴AE=DE=DF=AF ,
∵AF=4,
∴AE=DE=DF=AF=4,
∵DE∥AC ,
∴ ![]() ,
,
∵BD=6,AE=4,CD=3,
∴ ![]() ,
,
∴BE=8.
故选:D.
【考点精析】本题主要考查了线段垂直平分线的性质和平行线分线段成比例的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;三条平行线截两条直线,所得的对应线段成比例才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】问题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.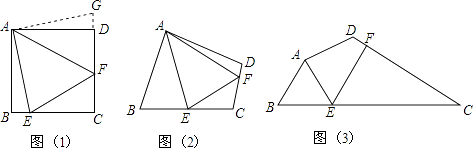
(1)【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图1证明上述结论.
(2)【类比引申】
如图2,四边形ABCD中∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD
(3)【探究应用】如图3,在某公园的同一水平面上,四条通道围成的ABCD,已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40( ![]() ,米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
,米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73).
=1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,AC=2,BD=2 ![]() ,AC,BD相交于点O.
,AC,BD相交于点O. 
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G. ①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
(1)求证:AC2=CDBC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB.
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( ) 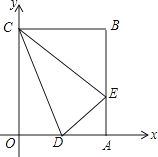
A.(3,1)
B.(3, ![]() )
)
C.(3, ![]() )
)
D.(3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形第四个顶点坐标的是( )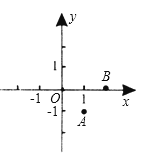
A.(3,-1)
B.(-1,-1)
C.(1,1)
D.(-2,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com