
【题目】已知代数式![]() ,当
,当![]() 时,该代数式的值为3.
时,该代数式的值为3.
(1)求c的值;
(2)已知:当![]() 时,该代数式的值为0.
时,该代数式的值为0.
①求:当![]() 时,该代数式的值;
时,该代数式的值;
②若![]() ,
,![]() ,
,![]() ,试比较a与d的大小,并说明理由.
,试比较a与d的大小,并说明理由.
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】①在数轴上没有点能表示![]() +1;②无理数是开不尽方的数;③存在最小的实数;④4的平方根是±2,用式子表示是
+1;②无理数是开不尽方的数;③存在最小的实数;④4的平方根是±2,用式子表示是![]() =±2;⑤某数的绝对值,相反数,算术平方根都是它本身,则这个数是0,其中正确的是______.
=±2;⑤某数的绝对值,相反数,算术平方根都是它本身,则这个数是0,其中正确的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
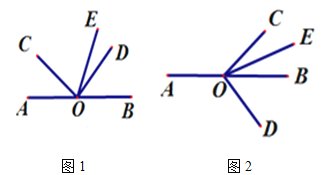
【题目】点O是直线AB上一点,∠COD是直角,OE平分∠BOC.
(1)①、如图1,若∠AOC=50°,求∠DOE的度数;
②、如图1,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);
(2)将图1中的∠COD按顺时针方向旋转至图2所示的位置.
探究∠AOC与∠DOE的度数之间的关系,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
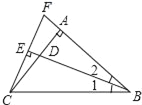
【题目】如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.CE=2,延长CE,BA交于点F.
(1)求证:△ADB≌△AFC;
(2)求BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金秋十月,长沙市某中学组织七年级学生去某综合实践基地进行秋季社会实践活动,每人需购买一张门票,该综合实践基地的门票价格为每张240元,如果一次购买500张以上(不含500张)门票,则门票价格为每张220元,请回答下列问题:
(1)列式表示n个人参加秋季社会实践活动所需钱数;
(2)某校用132000元可以购买多少张门票;
(3)如果我校490人参加秋季社会实践,怎样购买门票花钱最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD平分∠ABC,
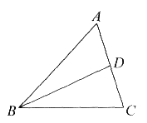
(1)作图:作BC边的垂直平分线分别交BC,BD于点E,F(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接CF,若∠A=60°,∠ABD=24°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;
x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;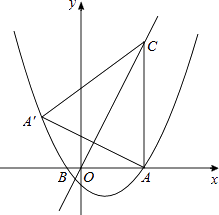
(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx经过A(4,0),B(1,3)两点,点B、C关于抛物线的对称轴l对称,过点B作直线BH⊥x轴,交x轴于点H.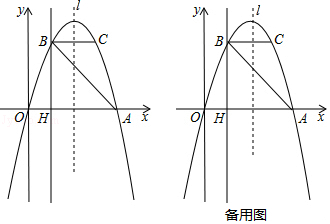
(1)求抛物线的解析式;
(2)若点M在直线BH上运动,点N在x轴上运动,是否存在这样的点M、N,使得以点M为直角顶点的△CNM是等腰直角三角形?若存在,请求出点M、N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com