

 时,S与t之间的函数关系式.
时,S与t之间的函数关系式. ;(2)①
;(2)① -2;②
-2;②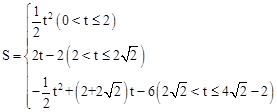 .
. ;(2)①由矩形的性质和已知AD∥BO,可得四边形ABOD是平行四边形,从而DO=AB=2,又由△DOI是等腰直角三角形可得OI=OD=2,从而由平移的性质可求得t=IM=OM-OI=
;(2)①由矩形的性质和已知AD∥BO,可得四边形ABOD是平行四边形,从而DO=AB=2,又由△DOI是等腰直角三角形可得OI=OD=2,从而由平移的性质可求得t=IM=OM-OI= -2;②首先确定当0<t≤
-2;②首先确定当0<t≤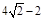 时,矩形EFGH沿y轴向上平移过程中关键点的位置,分0<t≤2,2<t≤
时,矩形EFGH沿y轴向上平移过程中关键点的位置,分0<t≤2,2<t≤ ,
, <t≤
<t≤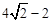 三种情况求出S与t之间的函数关系式.
三种情况求出S与t之间的函数关系式. .
. -2.
-2.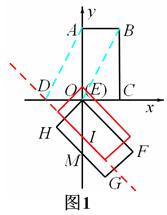
 ,F(
,F( ,-
,- ).
). ,
, .
. ,解得x=
,解得x=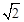 . ∴G(
. ∴G(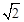 ,-
,-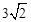 ).
).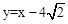 .
.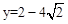 .
.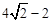 时,就是GF平移到过点C时的位置(如图5).
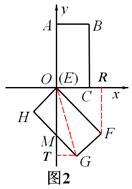
时,就是GF平移到过点C时的位置(如图5).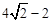 时,几个关键点如图3,4,5所示:
时,几个关键点如图3,4,5所示: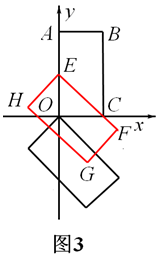
 ,此时,矩形EFGH沿y轴向上平移过程中边HG经过点O;
,此时,矩形EFGH沿y轴向上平移过程中边HG经过点O;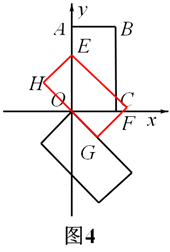
 ,此时,矩形EFGH沿y轴向上平移过程中边FG经过点C.
,此时,矩形EFGH沿y轴向上平移过程中边FG经过点C.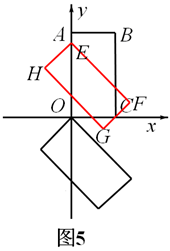
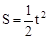 .
.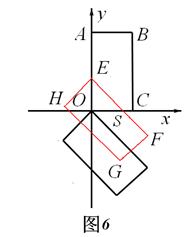
 时,矩形EFHG与矩形OABC重叠部分的面积为直角梯形OEPC的面积(如图7).此时OE= t,,OC=2.
时,矩形EFHG与矩形OABC重叠部分的面积为直角梯形OEPC的面积(如图7).此时OE= t,,OC=2.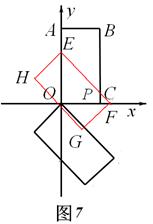
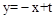 .
.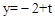 . ∴CP=
. ∴CP=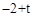 . ∴
. ∴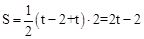 .
. <t≤
<t≤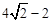 时,矩形EFHG与矩形OABC重叠部分的面积为五边形EQCUV的面积(如图8),
时,矩形EFHG与矩形OABC重叠部分的面积为五边形EQCUV的面积(如图8),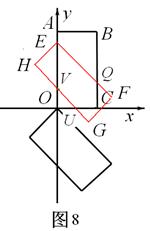
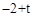 ,OU="OV=" t-
,OU="OV=" t- .
.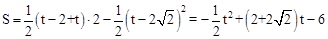 .
.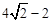 时,S与t之间的函数关系式为
时,S与t之间的函数关系式为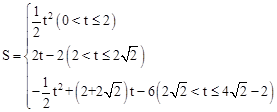 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
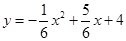 与直线
与直线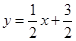 交于点A 、B,与y轴交于点C.
交于点A 、B,与y轴交于点C.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
|
若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )
|
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
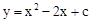 与y轴的交点为(0,﹣3),则下列说法不正确的是【 】
与y轴的交点为(0,﹣3),则下列说法不正确的是【 】| A.抛物线开口向上 |
| B.抛物线的对称轴是x=1 |
| C.当x=1时,y的最大值为﹣4 |
| D.抛物线与x轴的交点为(-1,0),(3,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com