
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=8cm,BC=10cm,AB=6cm,点Q从点A出发以1cm/s的速度向点D运动,点P从点B出发以2cm/s的速度向点C运动,P、Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s)
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=8cm,BC=10cm,AB=6cm,点Q从点A出发以1cm/s的速度向点D运动,点P从点B出发以2cm/s的速度向点C运动,P、Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s)分析 (1)先有运动速度表示出AQ,BP,即可得出结论;
(2)先判断出DQ=PC,建立方程求解即可得出结论;
(3)分两种情况讨论计算,求出时间,判断时间是否符合题意.
解答 解:(1)由运动知,AQ=t,BP=2t,
∵AD=8,BC=10,
∴DQ=AD-AQ=(8-t)(cm),PC=BC-BP=(10-2t)(cm),
故答案为(8-t)(cm),(10-2t)(cm);
(2)∵四边形PQDC是平行四边形,而AD∥BC,
∴DQ=PC,
由(1)知,DQ=8-t,PC=10-2t,
∴8-t=10-2t,
∴t=2,
即:t=2s时,四边形PQDC是平行四边形;
(3)由(1)知.AQ=t,BP=2t,DQ=(8-t)(cm),PC=(10-2t)(cm),
∵△DPQ是等腰三角形,且DQ≠DP,
∴①当DP=QP时,∴点P在DQ的垂直平分线上,
∴AQ+$\frac{1}{2}$DQ=BP,
∴t+$\frac{1}{2}$(8-t)=2t,
∴t=$\frac{8}{3}$,
②当DQ=PQ时,如图,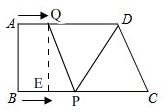
过点Q作QE⊥BC于E,
∴∠BEQ=∠OEQ=90°,
∵AD∥BC,∠B=90°,
∴∠A=∠B=90°,
∴四边形ABEQ是矩形,
∴EQ=AB=6,BE=AQ=t,
∴PE=BP-BE=t,
在Rt△PEQ中,PQ=$\sqrt{P{E}^{2}+E{Q}^{2}}$=$\sqrt{{t}^{2}+36}$,
∵DQ=8-t
∴$\sqrt{{t}^{2}+36}$=8-t,
∴t=$\frac{25}{4}$,
∵点P在边BC上,不和C重合,
∴0≤2t<10,
∴0≤t<5,
∴此种情况不符合题意,
即:t=$\frac{8}{3}$时,△DPQ是等腰三角形.
点评 此题是四边形综合题,主要考查了平行四边形的性质,线段的垂直平分线定理,勾股定理,矩形的判定和性质,解(2)的关键的关键是用DQ=PC建立方程求解,解(3)的关键是分情况讨论,是一道中等难度的题目.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
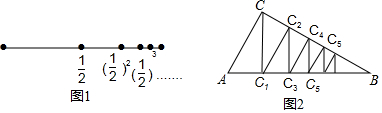
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a3÷2a=$\frac{3}{2}$a3 | B. | -0.00010=(-9999)0 | C. | a2•a3=a6 | D. | (-$\frac{1}{3}$)-2=9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
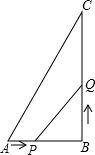 如图,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿BC边向点C以2cm/s的速度移动.经过2或4s,S△BPQ=8;△BPQ的面积的变化趋势是先增大后减小(或者:符合S=-(t-3)2+9),△BPQ的面积的最大值为9cm2.
如图,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿BC边向点C以2cm/s的速度移动.经过2或4s,S△BPQ=8;△BPQ的面积的变化趋势是先增大后减小(或者:符合S=-(t-3)2+9),△BPQ的面积的最大值为9cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
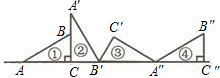 如图所示的直角三角形ABC向右翻滚,下列说法:(1)①到②是旋转;(2)①到③是平移;(3)①到④是平移;(4)②到③是旋转,其中正确的有( )
如图所示的直角三角形ABC向右翻滚,下列说法:(1)①到②是旋转;(2)①到③是平移;(3)①到④是平移;(4)②到③是旋转,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com