
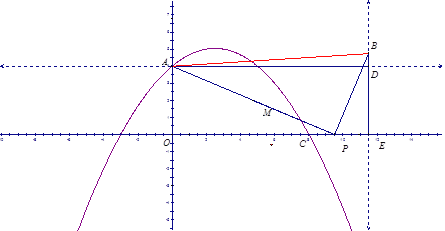
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Å×ĪļĻßy=ax2+![]() x+c¹żµćA£Ø0£¬4£©ŗĶC£Ø8£¬0£©£¬P£Øt£¬0£©ŹĒxÖįÕż°ėÖįÉĻµÄŅ»øö¶Æµć£¬MŹĒĻ߶ĪAPµÄÖŠµć£¬½«Ļ߶ĪMPČʵćPĖ³Ź±ÕėŠż×Ŗ90”ćµĆĻ߶ĪPB£®¹żµćB×÷xÖįµÄ“¹Ļß”¢¹żµćA×÷yÖįµÄ“¹Ļߣ¬Į½Ö±ĻßĻą½»ÓŚµćD£®
x+c¹żµćA£Ø0£¬4£©ŗĶC£Ø8£¬0£©£¬P£Øt£¬0£©ŹĒxÖįÕż°ėÖįÉĻµÄŅ»øö¶Æµć£¬MŹĒĻ߶ĪAPµÄÖŠµć£¬½«Ļ߶ĪMPČʵćPĖ³Ź±ÕėŠż×Ŗ90”ćµĆĻ߶ĪPB£®¹żµćB×÷xÖįµÄ“¹Ļß”¢¹żµćA×÷yÖįµÄ“¹Ļߣ¬Į½Ö±ĻßĻą½»ÓŚµćD£®
£Ø1£©Ēó“ĖÅ×ĪļĻߵĶŌ³ĘÖį£»
£Ø2£©µ±tĪŖŗĪÖµŹ±£¬µćDĀäŌŚÅ×ĪļĻßÉĻ£æ
£Ø3£©ŹĒ·ń“ęŌŚt£¬Ź¹µĆŅŌA”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷PEBĻąĖĘ£æČō“ęŌŚ£¬Ēó“ĖŹ±tµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ£Ø1£©¶Ō³ĘÖįĪŖ£ŗx=![]() £»£Ø2£©µ±t=3Ź±£¬µćDĀäŌŚÅ×ĪļĻßÉĻ£»£Ø3£©µ±t=©2+2
£»£Ø2£©µ±t=3Ź±£¬µćDĀäŌŚÅ×ĪļĻßÉĻ£»£Ø3£©µ±t=©2+2![]() ”¢t=8+4
”¢t=8+4![]() Ź±£¬ŅŌA”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷PEBĻąĖĘ£®
Ź±£¬ŅŌA”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷PEBĻąĖĘ£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾ŻĢāŅāĄūÓĆ“ż¶ØĻµŹż·ØĒó³öŗÆŹż½āĪöŹ½£¬“Ó¶ųµĆµ½¶Ō³ĘÖį£»£Ø2£©øł¾ŻĢāŅāµĆ³öµćMµÄ×ų±ź£¬øł¾ŻŠż×ŖµÄŠŌÖŹµĆ³öµćEŗĶµćBµÄ×ų±ź£¬“Ó¶ųµĆµ½µćDµÄ×ų±ź£¬Č»ŗóĒó³ötµÄÖµ£»£Ø3£©·Ö0£¼t£¼8ŗĶt£¾8Į½ÖÖĒéæö£¬ĆæÖÖĒéæö·ÖĮ½ÖÖĒéæö½ųŠŠĢÖĀŪ¼ĘĖć£¬µĆ³ötµÄÖµ£®
ŹŌĢā½āĪö£ŗ£Ø1£©ÓÉĢāµĆ£¬ £¬½āµĆ
£¬½āµĆ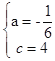 £®
£®
![]() Å×ĪļĻߵĽāĪöŹ½ĪŖ£ŗ
Å×ĪļĻߵĽāĪöŹ½ĪŖ£ŗ ![]() £¬ĖüµÄ¶Ō³ĘÖįĪŖ£ŗ
£¬ĖüµÄ¶Ō³ĘÖįĪŖ£ŗ ![]()
£Ø2£©ÓÉĢāŅāµĆ£ŗ ![]() £¬
£¬ ![]() £®
£®
![]() ŹĒ
ŹĒ![]() ČʵćPĖ³Ź±ÕėŠż×Ŗ90”ć¶ųµĆ£¬
ČʵćPĖ³Ź±ÕėŠż×Ŗ90”ć¶ųµĆ£¬ ![]()
![]() £¬
£¬ ![]() £®“Ó¶ųÓŠ
£®“Ó¶ųÓŠ![]() £®
£®
¼ŁÉč![]() ŌŚÅ×ĪļĻßÉĻ£¬ÓŠ
ŌŚÅ×ĪļĻßÉĻ£¬ÓŠ![]() £¬ ½āµĆ
£¬ ½āµĆ![]()
”ß![]() £¬¼“µ±
£¬¼“µ±![]() Ź±£¬µćDĀäŌŚÅ×ĪļĻßÉĻ£®
Ź±£¬µćDĀäŌŚÅ×ĪļĻßÉĻ£®
£Ø3£©¢Łµ±![]() Ź±£¬ČēĶ¼£¬
Ź±£¬ČēĶ¼£¬
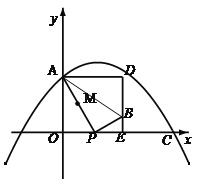
![]() £¬
£¬
£Ø1£©Čō”÷![]() ”×”÷ADB£¬“ĖŹ±
”×”÷ADB£¬“ĖŹ±![]() £¬ÓŠ£ŗ
£¬ÓŠ£ŗ ![]() £¬ £¬¼“
£¬ £¬¼“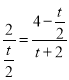 £¬
£¬
»Æ¼ņµĆ![]() £¬“ĖŹ±
£¬“ĖŹ±![]() ĪŽ½ā”£
ĪŽ½ā”£
Čō”÷![]() ”×”÷ADB£¬ “ĖŹ±
”×”÷ADB£¬ “ĖŹ±![]() £¬ÓŠ£ŗ
£¬ÓŠ£ŗ ![]() £¬ £¬¼“
£¬ £¬¼“ £¬
£¬
»Æ¼ņµĆ£ŗ ![]() £¬¹ŲÓŚ
£¬¹ŲÓŚ![]() µÄŅ»ŌŖ¶ž“Ī·½³ĢµÄÅŠ±šŹ½
µÄŅ»ŌŖ¶ž“Ī·½³ĢµÄÅŠ±šŹ½![]() £¬
£¬
ÓÉĒóøł¹«Ź½µĆ£ŗ![]()
![]() £¬
£¬ ![]() ”£
ӣ
¢Śµ±![]() Ź±£¬ČēĶ¼¢Ś£¬Čō”÷POA”×”÷ADB
Ź±£¬ČēĶ¼¢Ś£¬Čō”÷POA”×”÷ADB![]()
£Ø1£©Čō”÷![]() ”×”÷ADB£¬“ĖŹ±
”×”÷ADB£¬“ĖŹ±![]() £¬ÓŠ£ŗ
£¬ÓŠ£ŗ
![]() £¬¼“
£¬¼“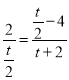 £¬»Æ¼ņµĆ
£¬»Æ¼ņµĆ![]() £¬½āµĆ
£¬½āµĆ![]() £ØøŗøłÉįČ„£©”£
£ØøŗøłÉįČ„£©”£
£Ø2£©Čō”÷![]() ”×”÷ADB£¬Ķ¬ĄķµĆ“ĖŹ±
”×”÷ADB£¬Ķ¬ĄķµĆ“ĖŹ±![]() ĪŽ½ā”£
ĪŽ½ā”£
×ŪŗĻÉĻŹö£ŗµ±![]() ”¢
”¢![]() Ź±£¬ŅŌA”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷PEBĻąĖĘ”£
Ź±£¬ŅŌA”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷PEBĻąĖĘ”£


 דŌŖ·»Č«³ĢĶ»Ęʵ¼Į·²āĻµĮŠ“š°ø
דŌŖ·»Č«³ĢĶ»Ęʵ¼Į·²āĻµĮŠ“š°ø Ö±ĶعóÖŻĆūŠ£ÖܲāŌĀæ¼Ö±ĶØĆūŠ£ĻµĮŠ“š°ø
Ö±ĶعóÖŻĆūŠ£ÖܲāŌĀæ¼Ö±ĶØĆūŠ£ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĮ½ĢõÖ±Ļß±»µŚČżĢõÖ±ĻßĖł½Ų£¬Čō”Ļ1ŗĶ”Ļ2ŹĒĶ¬ÅŌÄŚ½Ē£¬ĒŅ”Ļ1=75”ć£¬Ōņ”Ļ2ĪŖ£Ø £©
A.75”ć
B.105”ć
C.75”ć»ņ105”ć
D.“󊔲»Č·¶Ø
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶žŌŖŅ»“Ī·½³Ģ2x©y£½3£¬ÓĆŗ¬xµÄŹ½×Ó±ķŹ¾yµÄŠĪŹ½ŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ×Ō2009ğʚ£¬ĆæÄźµÄ11ŌĀ11ČÕŹĒTmallŅ»ÄźŅ»¶ČČ«³”“ó“ŁĻśµÄČÕ×Ó.ij·žŹĪµź¶ŌijÉĢĘ·ĶĘ³ö“ŁĻś»ī¶Æ:Ė«Ź®Ņ»µ±Ģģ£¬ĀņĮ½¼žµČÖµµÄÉĢĘ·æÉŌŚĆ漞Ō¼Ū¼õ50ŌŖµÄ»ł“”ÉĻ£¬ŌŁ“ņ°ĖÕŪ£»Čē¹ūµ„Āņ£¬Ōņ°“Ō¼Ū¹ŗĀņ.
£Ø1£©ÄŻÄŻæ“ÖŠĮ½¼žŌ¼Ū¶¼ŹĒ300ŌŖµÄ“ĖĄąÉĢĘ·£¬ ŌņŌŚĖ«Ź®Ņ»µ±Ģģ£¬¹ŗĀņÕāĮ½¼žÉĢĘ·×ܹ²ŠčŅŖ¶ąÉŁĒ®?
£Ø2£©ŠÜŠÜ¹ŗĀņĮĖĮ½¼žµČÖµµÄ“ĖĄąÉĢĘ·ŗó£¬ ·¢ĻÖ±ČĮ½¼žŅ»Ęš°“Ō¼ŪĮłÕŪ¹ŗĀņ±ćŅĖ. ČōÕāĮ½¼žµČÖµÉĢĘ·µÄ¼Ūøń¶¼ŹĒ“óÓŚ196µÄÕūŹż£¬ ŌņŌ¼ŪæÉÄÜŹĒ¶ąÉŁŌŖ?
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½Ćę×ų±ź×ų±źĻµ![]() ÖŠ£¬µć
ÖŠ£¬µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £¬µć
£¬µć![]() µÄ±ä»»µć
µÄ±ä»»µć![]() µÄ×ų±ź¶ØŅåČēĻĀ£ŗµ±
µÄ×ų±ź¶ØŅåČēĻĀ£ŗµ±![]() Ź±£¬µć
Ź±£¬µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £»µ±
£»µ±![]() Ź±£¬µć
Ź±£¬µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £®
£®
ŅŃÖŖµć![]() £¬µć
£¬µć![]() £¬µć
£¬µć![]() £®
£®
£Ø![]() £©µć
£©µć![]() µÄ±ä»»µć
µÄ±ä»»µć![]() µÄ×ų±źŹĒ__________£®
µÄ×ų±źŹĒ__________£®
µć![]() µÄ±ä»»µćĪŖ
µÄ±ä»»µćĪŖ![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬
£¬![]() £¬Ōņ
£¬Ōņ![]() __________£®
__________£®
£Ø![]() £©µć
£©µć![]() µÄ±ä»»µćĪŖ
µÄ±ä»»µćĪŖ![]() £¬Ėę×Å
£¬Ėę×Å![]() µÄ±ä»Æ£¬µć
µÄ±ä»Æ£¬µć![]() »įŌĖ¶ÆĘšĄ“£¬ĒėŌŚ±øÓĆĶ¼£Ø
»įŌĖ¶ÆĘšĄ“£¬ĒėŌŚ±øÓĆĶ¼£Ø![]() £©ÖŠ»³öµć
£©ÖŠ»³öµć![]() µÄŌĖ¶ÆĀ·¾¶£®
µÄŌĖ¶ÆĀ·¾¶£®
£Ø![]() £©Čō
£©Čō![]() ŹĒµČŃüČż½ĒŠĪ£¬ĒėÖ±½ÓŠ“³ö“ĖŹ±
ŹĒµČŃüČż½ĒŠĪ£¬ĒėÖ±½ÓŠ“³ö“ĖŹ±![]() µÄÖµ£ŗ__________£®
µÄÖµ£ŗ__________£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬ČōµćA£Ø©2£¬n£©£¬B£Ø1£¬©2£©ŹĒŅ»“ĪŗÆŹży=kx+bµÄĶ¼ĻóŗĶ·“±ČĄżŗÆŹży=![]() µÄĶ¼ĻóµÄĮ½øö½»µć£®
µÄĶ¼ĻóµÄĮ½øö½»µć£®
£Ø1£©Ē󷓱ȥżŗÆŹżŗĶŅ»“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ĒóÖ±ĻßABÓėxÖįµÄ½»µćCµÄ×ų±ź£»
£Ø3£©ĒóµćOµ½Ö±ĻßABµÄ¾ąĄė£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£y3n+1”Āyn+1£½__________£¬[(£m)3]2£½___________;
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”潫Źż420000ÓĆæĘѧ¼ĒŹż·Ø±ķŹ¾ĪŖ£Ø””””£©
A. 420”Į103B. 42”Į104C. 4.2”Į105D. 0.42”Į106
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÕż±ČĄżŗÆŹży=(2m+4)x£¬Ēó£ŗ
(1)mĪŖŗĪÖµŹ±£¬ŗÆŹżĶ¼Ļó¾¹żµŚŅ»”¢ČżĻóĻŽ£æ
(2)mĪŖŗĪÖµŹ±£¬yĖęxµÄŌö“ó¶ų¼õŠ”£æ
(3)mĪŖŗĪÖµŹ±£¬µć(1£¬3)ŌŚøĆŗÆŹżµÄĶ¼ĻóÉĻ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com