
【题目】已知线段AB=4.8cm,点C是线段AB的中点,点D是线段CB的中点,点E在线段AB上,且CE=![]() AC,画图并计算DE的长.
AC,画图并计算DE的长.
【答案】DE的长为2cm或0.4cm.
【解析】
分点E在线段AC上及点E在线段BC上两种情况考虑:
(1)当点E在线段AC上时,根据AB的长度及点C、D分别是线段AB、CB的中点,即可得出CD、CE的长度,将其代入DE=CD+CE中即可求出DE的长;
(2)当点E在线段CB上时,根据AB的长度及点C、D分别是线段AB、CB的中点,即可得出CD、CE的长度,将其代入DE=CD-CE中即可求出DE的长.综上即可得出结论.
(1)当点E在线段AC上时,如图1所示.
∵AB=4.8cm,点C是线段AB的中点,
∴AC=BC=![]() AB=2.4cm.
AB=2.4cm.
∵点D是线段CB的中点,
∴CD=![]() BC=1.2cm.
BC=1.2cm.
又∵CE=![]() AC,
AC,
∴CE=0.8cm,
∴DE=CD+CE=1.2+0.8=2(cm).
(2)当点E在线段BC上时,如图2所示.
∵AB=4.8cm,点C是线段AB的中点,
∴AC=BC=![]() AB=2.4cm.
AB=2.4cm.
∵点D是线段CB的中点,
∴CD=![]() BC=1.2cm.
BC=1.2cm.
又∵CE=![]() AC,
AC,
∴CE=0.8cm,
∴DE=CD﹣CE=1.2﹣0.8=0.4(cm).
综上所述:DE的长为2cm或0.4cm.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如同,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由 ![]() ,线段CD和线段BD所围成图形的阴影部分的面积为 .
,线段CD和线段BD所围成图形的阴影部分的面积为 . 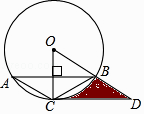
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条直线分别与直线BE、直线CE、直线CF、直线BF相交于点A,G,D,H且∠1=∠2,∠B=∠C
(1)找出图中相互平行的线,说说它们之间为什么是平行的;
(2)证明:∠A=∠D.
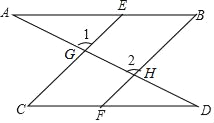
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.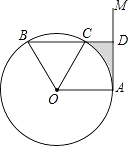
(1)求证:AM是⊙O的切线;
(2)若DC=2,求图中阴影部分的面积(结果保留π和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D. 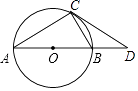
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB= ![]() CD,求⊙O半径.
CD,求⊙O半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=![]() ∠AOC.
∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( ) 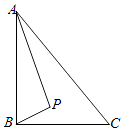
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E. 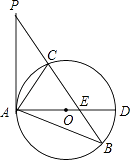
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点C,若ACAB=12,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com