
【题目】如图,EG⊥BC于点G,AD⊥BC于点D,∠1=∠E,请证明AD平分∠BAC.
科目:初中数学 来源: 题型:
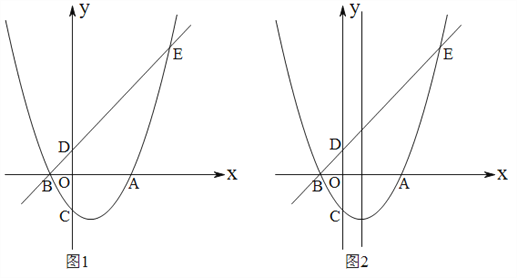
【题目】已知,如图1:抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,对称轴为直线
,对称轴为直线![]() ,且过点
,且过点![]() .
.
(1)求出抛物线的解析式及![]() 点坐标,
点坐标,
(2)点![]() ,
, ![]() ,作直线
,作直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的点,连接
下方抛物线上的点,连接![]() 、
、![]() ,求
,求![]() 的面积的最大值,并求出此时点
的面积的最大值,并求出此时点![]() 的坐标;
的坐标;
(3)点![]() 、
、![]() 是抛物线对称轴上的两点,且已知
是抛物线对称轴上的两点,且已知![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ,
, ![]() ),当
),当![]() 为何值时,四边形
为何值时,四边形![]() 周长最小?并求出四边形
周长最小?并求出四边形![]() 周长的最小值,请说明理由.
周长的最小值,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进10m到达点D处,又测得点A的仰角为60°,那么建筑物AB的高度是________ m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
(1)估计从袋中任意摸出一个球,恰好是红球的概率是多少?
(2)请你估计袋中红球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
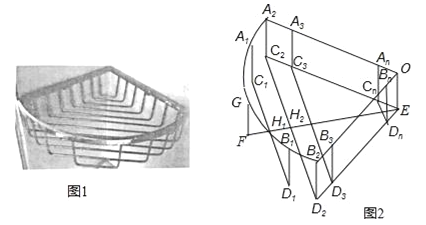
【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在![]() 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com