
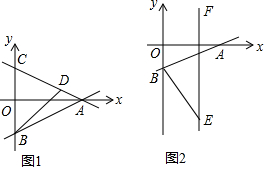
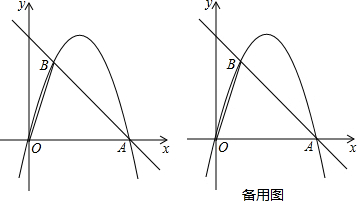
 ��ֱ֪��l1��y=$\frac{1}{2}$x-2��x�ύ�ڵ�A����y�ύ�ڵ�B����ֱ����x�ᷭ�ۣ��õ�һ���º�����ͼ��l2��ͼ1����ֱ��l2��y�ύ�ڵ�C��
��ֱ֪��l1��y=$\frac{1}{2}$x-2��x�ύ�ڵ�A����y�ύ�ڵ�B����ֱ����x�ᷭ�ۣ��õ�һ���º�����ͼ��l2��ͼ1����ֱ��l2��y�ύ�ڵ�C������ ��1�������۵��ó���C�����꣬�����ó����ۣ�
��2������������������ε������ʽ���ɵó�������ϵʽ��
��3�������ù��ɶ������涨�������жϳ����ۣ�
�����жϳ���A1B1P�ǵ���ֱ�������Σ�ֻ��ֱ��A1B1��y��Ľ���Ϊֱ�Ƕ��㣬�����ƶ���ʲôλ�ã�Ҫʹ��A1B1P�ǵ���ֱ�������Σ����С�A1OB1�ա�B1HP
���ݢ��ص㣬Ҫʹ�á�A1B1P�ǵ���ֱ�������Σ�ֱ��ABƽ������͵�Pƽ�Ƶ������ͬ�����ɵó����ۣ�
��� �⣺��1����ֱ��l1��y=$\frac{1}{2}$x-2��x�ύ�ڵ�A����y�ύ�ڵ�B��
��A��4��0����B��0��-2����
�߽�ֱ����x�ᷭ�ۣ��õ�һ���º�����ͼ��l2��ֱ��l2��y�ύ�ڵ�C��
��C��0��2����
��A��4��0����
��ֱ��AC�Ľ���ʽΪy=-$\frac{1}{2}$x+2��
��2����ͼ2���ɣ�1��֪��ֱ��AC�Ľ���ʽΪy=-$\frac{1}{2}$x+2��
��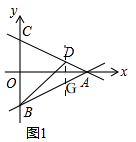 ��ֱ��AC��һ����D��x��y����
��ֱ��AC��һ����D��x��y����
��D��x��-$\frac{1}{2}$x+2��
����D��DG��OA��
��ֱ��l1��y=$\frac{1}{2}$x-2��
��G��x��$\frac{1}{2}$x-2����
��DG=|-$\frac{1}{2}$x+2-��$\frac{1}{2}$x-2|=|x-4|
�ٵ�x��4ʱ��DG=x-4��xA-xD=xD-xA��
��S=S��BDG-S��ADG=$\frac{1}{2}$DG��xD-��$\frac{1}{2}$DG����xD-xA��=$\frac{1}{2}$DG��xA=$\frac{1}{2}$��x-4����4=2x-4��
�ڵ�x��4ʱ��DG=4-x��|xA-xD|=xA-xD��
��S=$\frac{1}{2}$DG��|xD|+$\frac{1}{2}$DG��|xA-xD|=$\frac{1}{2}$DG��xA=$\frac{1}{2}$��4-x����4=8-2x��
��S=$\left\{\begin{array}{l}{8-2x��x��4��}\\{2x-8��x��4��}\end{array}\right.$��
��3�����ɣ�1��֪��A��4��0����B��0��-2����
��E��2��-6����
��AB2=20��AE2=40��BE2=20��
��AB=BE��AE2=AB2+BE2��
���ABE�ǵ���ֱ�������Σ�
�ڴ��ڣ�
���ɣ���ͼ2��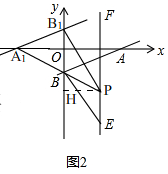
��AB����ֱEF��
��ƽ�ƵĹ����У�ʹ�á�A1B1P�ǵ���ֱ�������Σ���B1A1P��90�㣬
������A1��������ֱ�Ƕ��㣬��PҲ��������ֱ�Ƕ��㣬
��ֻ�е�B1��ֱ�Ƕ��㣬
��B1P=B1A1��
�ߡ�A1B1O+��PB1H=90�㣬��A1B1O+��OA1B1=90�㣬
���OA1B1=��PB1H��
�ڡ�A1OB1�͡�B1HP�У�$\left\{\begin{array}{l}{��{A}_{1}O{B}_{1}=��{B}_{1}HP}\\{��O{A}_{1}{B}_{1}=��H{B}_{1}P}\\{{A}_{1}{B}_{1}={B}_{1}P}\end{array}\right.$��
���A1OB1�ա�B1HP��
��B1H=A1B1��OB1=HP=2��
��B1��0��-2����0��2����
����B1��0��-2��ʱ���Ǣٵ������P��2��-6����
����B1��0��2��ʱ��
��B��0��-2����
��ֱ��AB����ƽ��4����λ��
���PҲ����ƽ��4����λ��
��P��2��-2����
��P��2��-6����2��-2����
���� ������һ�κ����ۺ��⣬��Ҫ�������۵������ʣ�ȫ�������ε��ж������ʣ������ε������ʽ������ֱ�������ε����ʣ��жϡ�A1OB1�ա�B1HP�ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
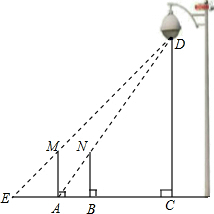 һ�����ϣ��������������õƹ��µ�Ӱ�ӳ�������һ·��D�ĸ߶ȣ���ͼ���������ߵ���A��ʱ�������������ֱ��ʱ����AM��Ӱ�ӳ�AE������ȣ�����������AC���������ǰ�ߣ��ߵ���B��ʱ������ֱ��ʱ����BN��Ӱ��ǡ�����߶�AB�������AB=1.25m����֪����ֱ��ʱ������Ϊ1.75m����·�Ƶĸ�CD�ij����������ȷ��0.1m����
һ�����ϣ��������������õƹ��µ�Ӱ�ӳ�������һ·��D�ĸ߶ȣ���ͼ���������ߵ���A��ʱ�������������ֱ��ʱ����AM��Ӱ�ӳ�AE������ȣ�����������AC���������ǰ�ߣ��ߵ���B��ʱ������ֱ��ʱ����BN��Ӱ��ǡ�����߶�AB�������AB=1.25m����֪����ֱ��ʱ������Ϊ1.75m����·�Ƶĸ�CD�ij����������ȷ��0.1m�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | -2 | C�� | 2 | D�� | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
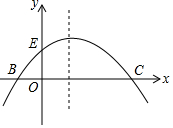 ��ͼ����֪������y=-$\frac{1}{m}$��x+2����x-m��������m��0����x�ύ�ڵ�B��C����B�ڵ�C����ࣩ����y�ύ�ڵ�E��
��ͼ����֪������y=-$\frac{1}{m}$��x+2����x-m��������m��0����x�ύ�ڵ�B��C����B�ڵ�C����ࣩ����y�ύ�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com