
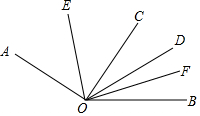
 如图,已知∠AOB内部有顺次的四条射线:OE、OC、OD、OF、OE平分∠AOC,OF平分∠DOB
如图,已知∠AOB内部有顺次的四条射线:OE、OC、OD、OF、OE平分∠AOC,OF平分∠DOB分析 (1)(2)通过角的和差关系角平分线的性质,得到∠EOF与已知角∠AOB、∠AOC的关系,代入求值;
(3)根据(1)(2)的结论,得出规律.
解答 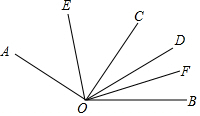 解:(1)∵∠EOF=∠EOC+∠DOC+∠FOD
解:(1)∵∠EOF=∠EOC+∠DOC+∠FOD
=$\frac{1}{2}$∠AOC+∠COD+$\frac{1}{2}$∠BOD
=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠COD
∵∠AOB=160°,∠DOC=40°
∴∠EOF=80°+20°=100°.
(2),∵∠EOF=∠EOC+∠DOC+∠FOD
=$\frac{1}{2}$∠AOC+∠COD+$\frac{1}{2}$∠BOD
=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠COD
∵∠AOB=a,∠COD=β,
∴∠EOF=$\frac{1}{2}α$+$\frac{1}{2}β$=$\frac{1}{2}(α+β)$.
(3)若∠AOB内部有顺次的四条射线:OE、OC、OD、OF,OE平分∠AOC,OF平分∠DOB,
那么∠EOF=$\frac{1}{2}(∠AOB+∠COD)$.
点评 本题考查了角平分线的性质及角的和差关系.通过和差关系角平分线的性质得到∠EOF=$\frac{1}{2}(∠AOB+∠COD)$是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
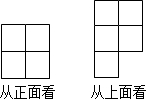 用若干大小相同的小正方块搭一个几何体,使得从正面和从上面看到的这个几何体的形状如图所示,那么搭这样一个几何体最少需要多少个小正方块( )
用若干大小相同的小正方块搭一个几何体,使得从正面和从上面看到的这个几何体的形状如图所示,那么搭这样一个几何体最少需要多少个小正方块( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com