
分析 (1)设一名环卫工人每小时清雪x立方米,则一台清雪机每小时清雪200x立方米.等量关系为:一台清雪机清理9000立方米的积雪所用时间=150名环卫工人清理这些积雪所用时间-2小时,依此列出方程,解方程即可;
(2)设市政府又调配了y台清雪机,2台清雪机和300名环卫工人工作3小时的清雪量+(y+2)台清雪机和300名环卫工人工作4小时的清雪量≥54750立方米,依此列出不等式,解不等式即可.
解答 解:(1)设一名环卫工人每小时清雪x立方米,则一台清雪机每小时清雪200x立方米.根据题意得
$\frac{9000}{200x}=\frac{9000}{150x}-2$,
解得x=7.5,
经检验x=7.5是原方程的解,
当x=7.5时,200x=1500.
答:一台清雪机每小时清雪1500立方米;
(2)3(1500×2+7.5×300)=15750(立方米).
设市政府又调配了y台清雪机.根据题意得
15750+(7-3)[1500(y+2)+300×7.5]≥54750,
解得y≥3.
答:市政府最少又调配了3台清雪机才能完成任务.
点评 本题考查分式方程及一元一次不等式的应用,分析题意,找到合适的等量关系与不等关系是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
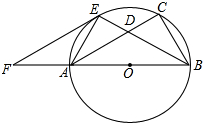 如图,已知以Rt△ABC的斜边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的斜边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com