
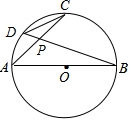
 已知:如图AB为⊙O的直径,弦AC、BD相交于点P,
已知:如图AB为⊙O的直径,弦AC、BD相交于点P,分析 (1)先根据圆周角定理得出∠B=∠C,进而可得出结论;
(2)设AP=x,则PC=AC-x=2-x,再由相似三角形的性质即可得出结论.
解答 解:(1)△ABP∽△DCP.
理由:∵∠B=∠C,∠APB=∠DPC,
∴△ABP∽△DCP;
(2)设AP=x,则PC=AC-x=2-x,
∵设AP=x,则PC=AC-x=2-x,
∴$\frac{AP}{PC}$=$\frac{CD}{AB}$,即$\frac{x}{2-x}$=$\frac{3}{1}$,
解得x=$\frac{3}{2}$,
即AP=$\frac{3}{2}$.
点评 本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.


科目:初中数学 来源: 题型:解答题
 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售量x(千克) | 销售价c(元) |
| 1 | 2+0.1 |
| 2 | 4+0.2 |
| 3 | 6+0.3 |
| 4 | 8+0.4 |
| … | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com