
| A.1个 | B.2个 | C.3个 | D.4个 |
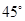 ,所以所有的等腰三角形的三个角都相等,所以它们是相似三角形;(4) 所有定理的逆命题都是真命题,定理的逆命题不一定是真命题,可能是假命题;对顶角相等,其逆命题为如果两个角相等,那么这两个角是对顶角,不一定正确,它可能是同位角,或者其他角都可以;所以(1)(2)(3)是正确的
,所以所有的等腰三角形的三个角都相等,所以它们是相似三角形;(4) 所有定理的逆命题都是真命题,定理的逆命题不一定是真命题,可能是假命题;对顶角相等,其逆命题为如果两个角相等,那么这两个角是对顶角,不一定正确,它可能是同位角,或者其他角都可以;所以(1)(2)(3)是正确的

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源:不详 题型:解答题
 ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
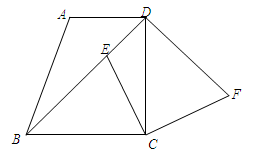
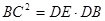 时,试判断四边形DECF的形状,并说明理由.
时,试判断四边形DECF的形状,并说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
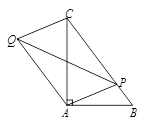
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.周长相等的锐角三角形都全等 |
| B.周长相等的直角三角形都全等 |
| C.周长相等的钝角三角形都全等 |
| D.周长相等的等腰直角三角形都全等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com