
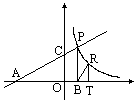
如图,直线y=![]() x+2分别交x、y轴于A、C,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,S△ABP=9.(1)求点P的坐标;(2)设点R与点P在同一反比例函数的同一支图像上,且点正在直线PB的右侧,作RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
x+2分别交x、y轴于A、C,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,S△ABP=9.(1)求点P的坐标;(2)设点R与点P在同一反比例函数的同一支图像上,且点正在直线PB的右侧,作RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
|
解答: (1)根据己知条件可得A点坐标为(-4,0),C点坐标为(0,2),即OA=4,OC=2.又∵ S△ABP=9,∴AB·BP=18.又∵ PB⊥x轴,∴OC∥PB,∴△AOC∽△ABP.∴ ∴ 2BP2=18,BP=3,AB=6,P点坐标为(2,3).(2)设R点的坐标为(x,y). ∵ P点坐标为(2,3),∴反比例函数的解析式为y=∵△ BPT与△AOC相似,∠AOC=∠BTR=∴ 若 ∴  解得 解得  (不合题意,舍去) (不合题意,舍去)
若
 解得 解得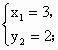  (不合题意,舍去) (不合题意,舍去)
∴满足条件的 R的坐标为(3,2),(分析: (1)由于P点在直线,y=(2)由于△AOC是直角三角形,且两直角边长都可求出,△BRT也是直角三角形,只要两条直角边对应成比例,两个直角三角形即可相似. |


科目:初中数学 来源: 题型:
(11·漳州)(满分13分)如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD.
(1)填空:点C的坐标是(_ ▲ ,_ ▲ ),
点D的坐标是(_ ▲ ,_ ▲ );
(2)设直线CD与AB交于点M,求线段BM的长;
(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,
请求出所有满足条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012届黑龙江大庆初三模拟数学试卷三(带解析) 题型:解答题
如图,直线y=x-1和抛物线y=x 2+bx+c都经过点A(1,0),B(3,2).
【小题1】求抛物线的解析式;
【小题2】求不等式x2+bx+c<x-1的解集(直接写出答案).
【小题3】设直线AB交抛物线对称轴与点D,请在对称轴上求一点P(D点除外),使△PBD为等腰三角形.(直接写出点P的坐标,不写过程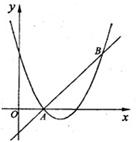
查看答案和解析>>
科目:初中数学 来源:2013届山东省济宁地区九年级第一学期期末考试数学试卷(带解析) 题型:解答题
如图,直线y=2x-2与x轴交于点A,抛物线y=ax2+bx+c的对称轴是直线x=3,抛物线经过点A,且顶点P在直线y=2x-2上.
(1)求A、P两点的坐标及抛物线y=ax2+bx+c的解析式;
(2)画出抛物线的草图,并观察图象写出不等式ax2+bx+c>0的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com