
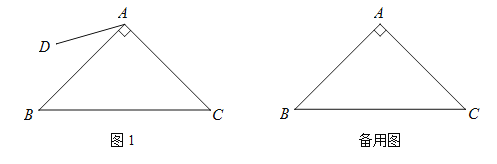
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)请根据题意补全图1;
(2)猜测BD和CE的数量关系并证明;
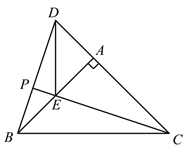
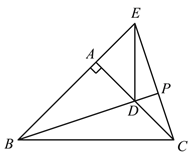
(3)作射线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,补全图形,直接写出PB的长.
【答案】(1)答案见解析;(2)BD=CE;(3)PB的长是![]() 或
或![]() .
.
【解析】试题分析:(1)根据题意画出图形即可;(2)根据“SAS”证明△ABD≌△ACE,从而可得BD=CE;(3)①根据“SAS”可证△ABD≌△ACE,从而得到∠ABD=∠ACE,再由两角对应相等的两个三角形相似可证△ACD∽△PBE,列比例方程可求出PB的长;②与①类似,先求出PD的长,再把PD和BD相加.
解:(1)如图
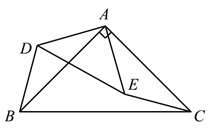
(2)BD和CE的数量是:BD=CE ;
∵∠DAB+∠BAE=∠CAE+∠BAE=90°,∴∠DAB=∠CAE.
∵AD=AE,AB=AC,∴△ABD≌△ACE,∴BD=CE.
(3)①CE=![]() .
.
∵△ABD≌△ACE, ∴∠ABD=∠ACE,
∴△ACD∽△PBE,
![]() ,
,
∴![]() ;
;
②∵△ABD∽△PDC,
![]() ,
,
∴![]() ;
;
∴PB=PD+BD=![]() .
.
∴PB的长是![]() 或
或![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E、F是对角线BD上的两点,且BE=DF.

(1)求证:四边形AECF是平行四边形.
(2)如果四边形ABCD是菱形,求证:四边形AECF也是菱形.
(3)如果四边形ABCD是矩形,请判断四边形AECF的形状,不必写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴上,点![]() 的初始位置表示的数为
的初始位置表示的数为![]() ,现点
,现点![]() 做如下移动,第1次点
做如下移动,第1次点![]() 向左移动3个单位长度至点
向左移动3个单位长度至点![]() ,第2次从点
,第2次从点![]() 向右移动6个单位长度至点
向右移动6个单位长度至点![]() ,第
,第![]() 次从点
次从点![]() 向左移动
向左移动![]() 个单位长度至点
个单位长度至点![]() ,…,按照这种移动方式进行下云,如果点
,…,按照这种移动方式进行下云,如果点![]() 与原点的距离不小于
与原点的距离不小于![]() ,那么
,那么![]() 的最小值是___.
的最小值是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两仓库分别有水泥
两仓库分别有水泥![]() 吨和
吨和![]() 吨,
吨,![]() 、
、![]() 两工地分别需要水泥
两工地分别需要水泥![]() 吨和
吨和![]() 吨.已知从
吨.已知从![]() 、
、![]() 仓库到
仓库到![]() 、
、![]() 工地的运价如下表:
工地的运价如下表:
到 | 到 | |
| 每吨 | 每吨 |
| 每吨 | 每吨 |
1)若从![]() 仓库运到
仓库运到![]() 工地的水泥为
工地的水泥为![]() 吨,则用含
吨,则用含![]() 的代数式表示从
的代数式表示从![]() 仓库运到
仓库运到![]() 工地的水泥为_____吨,从
工地的水泥为_____吨,从![]() 仓库将水泥运到
仓库将水泥运到![]() 工地的运输费用为______元;
工地的运输费用为______元;
(2)求把全部水泥从![]() 、
、![]() 两仓库运到
两仓库运到![]() 、
、![]() 两工地的总运输费(用含
两工地的总运输费(用含![]() 的代数式表示并化简);
的代数式表示并化简);
(3)如果从![]() 仓库运到
仓库运到![]() 工地的水泥为
工地的水泥为![]() 吨时,那么总运输费为多少元?
吨时,那么总运输费为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球每筒的售价多15元,健民体育活动中心从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据健民体育活动中心消费者的需求量,活动中心决定用不超过2550元钱购进甲、乙两种羽毛球共50筒,那么最多可以购进多少筒甲种羽毛球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点M在BA的延长线上,MD切⊙O于点D,过点B作BN⊥MD于点C,连接AD并延长,交BN于点N.
(1)求证:AB=BN;
(2)若⊙O半径的长为3,cosB=![]() ,求MA的长.
,求MA的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一个产品销售点在经销某著名特色小吃时发现:如果每箱产品赢利10元,每天可销售50箱,若每箱产品涨价1元,日销量将减少2箱.
(1)现该销售点为使每天赢利600元,同时又要顾客得到实惠,那么每箱产品应涨价多少元?
(2)若该销售点单纯从经济角度考虑,每箱产品应涨价多少元?才能使每天的盈利最高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com