
����Ŀ���������ձ�ȫ����������������ڼ䣬����ij�ձ���ƽ��ÿ�������300���ձ�������1���ձ���������1Ԫ�������鷢�֣����۵���ÿ��0.1Ԫ��ƽ��ÿ��ɶ�����100����Ϊ��ʹÿ���ȡ��������࣬�õ���������۵����½�m��0��m��1��Ԫ
��1�����۵����½�mԪ��ÿ���ձ�������Ϊ����Ԫ���õ�ƽ��ÿ��������������ձ����ú�m�Ĵ���ʽ��ʾ���軯��
��2���ڲ������������ص������£���m��Ϊ����ʱ������ʹ�õ�ÿ���ȡ��������420Ԫ�����������ձ����ࣿ
���𰸡�(1) ��1��m��Ԫ����300+1000m����;(2) 0.4, 420Ԫ.
�������������������1����������ʽ���ɵ��½�mԪ��ÿ���ձ�������Ϊ(1-m)Ԫ���ٸ���ÿ�½�0.1Ԫ�ɶ�����100������ȷ����ÿ���������300+1000m�����ձ���
��2�����������г����̣�������̵Ľ⼴�ɵõ������
�����������1��ÿ��������Ϊ��1��m��Ԫ��
ÿ��������ձ���300+![]() ����������300+1000m������
����������300+1000m������
��2����1��m����300+1000m��=420��
����ã�100m2��70m+12=0��
����m2��0.7m+0.12=0��
���m=0.4��m=0.3��
�ɵã���m=0.4ʱ�������ձ����࣬
�𣺵�m��Ϊ0.4ʱ������ʹ�̵�ÿ�����۸��ձ���ȡ��������420Ԫ�����������ձ�����.


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ������x�ύ��ĺ�����ֱ�Ϊ-1��3�����н��ۣ�
��b-2a=0����a��2b+4c��0����abc��0����8a+c��0.
������ȷ���У� ��
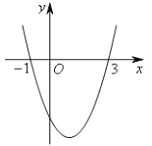
A. 3�� B. 2�� C. 1�� D. 0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� |a |3�� |b| 1 ���� a b ����ô a b ��ֵ�ǣ� ��
A. 4B. 2C. 4D. 4��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ����( )
A. a2+a4=a6B. 3(a-b)=3a-bC. (a2)4=a6D. a2-2a2=-a2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��
��a+b����a��b��+��a��b��2����2a2��ab��������a��b��һԪ���η���x2+x��2=0������ʵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ����D�ǻ�AB��һ�㣬C�ǻ�AD���е㣬����C��AB�Ĵ��ߣ���AB
��E�������D�����߽��ڵ�G������AD���ֱ�CE��CB�ڵ�P��Q������AC���������н��ۣ���
��BAD=��ABC����GP=GD���۵�P�ǡ�ACQ�����ģ�������ȷ������_______������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����²���.
��ͼ����֪������ABCD�ĶԽ���AC��BD�ڵ�O��E��AC��һ�㣬AG��BE������ΪG.��֤��OE=OF.
֤�������ı���ABCD��������.
���BOE=��AOF=90��,��OA=OE.
�֡�AG��BE�����1+��3��90������2+��3������1����2.
��Rt��BOE��Rt��AOF,��OE=OF.

�Ÿ���������⣬����֤��˼·�ĺ��������� ʹ������Խ������֤�������еĹؼ���֤�� .
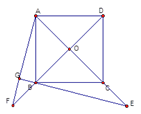
�������������Ϊ����E��AC���ӳ����ϣ�AG��BE��EB���ӳ����ڵ�G���ӳ�AG��DB���ӳ����ڵ�F����ͼ��������������.
��֤��OF=OE.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com