
【题目】
在平面直角坐标系中,已知抛物线![]() +n过点A(4,0),B (1,-3).
+n过点A(4,0),B (1,-3).

(1)求抛物线的表达式及顶点D的坐标;
(2)将![]() 时函数的图象记为G,点P为G上一动点,求P点纵坐标
时函数的图象记为G,点P为G上一动点,求P点纵坐标![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若经过点C(4,-4)的直线![]() 与图象G有两个公共点,结合图象直接写出b的取值范围.
与图象G有两个公共点,结合图象直接写出b的取值范围.
科目:初中数学 来源: 题型:
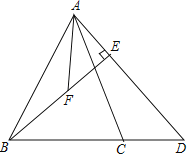
【题目】如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
(1)若AC=![]() ,AE=
,AE=![]() ,求BE的长;
,求BE的长;
(2)在(1)的条件下,如果∠D=45°,求△ABD的面积.
(3)若∠BAC=∠DAF,求证:2AF=AD;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,CE是∠DCB的平分线,F是AB的中点,AB=6,BC=5,则AE:EF:FB为( )

A. 1:2:3 B. 2:1:3 C. 3:2:1 D. 3:1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,则①CA平分∠BCD;②AC⊥BD;③∠ABC=∠ADC=90°;④四边形ABCD的面积为ACBD.上述结论正确的个数是( )

A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知![]() 是⊙
是⊙![]() 的直径,
的直径, ![]() 是
是![]() 上的一个动点(点
上的一个动点(点![]() 与点
与点![]() 、
、![]() 不重合),连接
不重合),连接![]() .
. ![]() 是
是![]() 的中点,作弦
的中点,作弦![]() ,垂足为
,垂足为![]() .
.
(![]() )若点
)若点![]() 和点
和点![]() 不重合,连接
不重合,连接![]() 、
、![]() 和
和![]() .当
.当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的度数.
的度数.
(![]() )若点
)若点![]() 和点
和点![]() 重合,如图②.探索
重合,如图②.探索![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
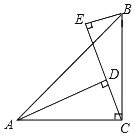
【题目】已知:如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D,E.
(1)求证:△BEC≌△CDA;
(2)当AD=3,BE=1时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题:

(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?
(2)已知洗衣机的排水速度为每分钟19升.
①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式;
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并完成以下证明:
已知:点P在直线CD上,∠BAP+∠APD=180°,∠1=∠2.
求证:AB∥CD,∠E=∠F.
证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥ .( )
∴∠BAP= .( )
又∵∠1=∠2,(已知)
∠3= ﹣∠1,
∠4= ﹣∠2,
∴∠3= (等式的性质)
∴AE∥PF.( )
∴∠E=∠F.( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com