
【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为 . 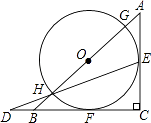
【答案】![]() a
a
【解析】解:如图,连接OE、OF, 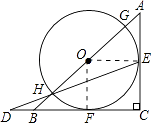
∵由切线的性质可得OE=OF=⊙O的半径,∠OEC=∠OFC=∠C=90°,
∴OECF是正方形,
∵由△ABC的面积可知 ![]() ×AC×BC=
×AC×BC= ![]() ×AC×OE+
×AC×OE+ ![]() ×BC×OF,
×BC×OF,
∴OE=OF= ![]() a=EC=CF,BF=BC﹣CF=0.5a,GH=2OE=a,
a=EC=CF,BF=BC﹣CF=0.5a,GH=2OE=a,
∵由切割线定理可得BF2=BHBG,
∴ ![]() a2=BH(BH+a),
a2=BH(BH+a),
∴BH= ![]() a或BH=
a或BH= ![]() a(舍去),
a(舍去),
∵OE∥DB,OE=OH,
∴△OEH∽△BDH,
∴ ![]() ,
,
∴BH=BD,CD=BC+BD=a+ ![]() a=
a= ![]() a.
a.
故答案为: ![]() a.
a.
连接OE、OF,由切线的性质结合结合直角三角形可得到正方形OECF,并且可求出⊙O的半径为0.5a,则BF=a﹣0.5a=0.5a,再由切割线定理可得BF2=BHBG,利用方程即可求出BH,然后又因OE∥DB,OE=OH,利用相似三角形的性质即可求出BH=BD,最终由CD=BC+BD,即可求出答案.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】双胞胎兄弟小明和小亮在同一班读书,周五16:00时放学后,小明和同学走路回家,途中没有停留,小亮骑车回家,他们各自与学校的距离s(米)与用去的时间t(分)的关系如图所示,根据图象提供的有关信息,下列说法中错误的是( )

A. 兄弟俩的家离学校1000米
B. 他们同时到家,用时30分
C. 小明的速度为50米/分
D. 小亮中间停留了一段时间后,再以80米/分的速度骑回家
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=68°,∠2=68°,∠3=112°.在下列解答中,填空:
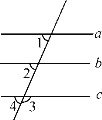
(1)因为∠1=68°,∠2=68°(已知),
所以__________(等量代换).
所以____∥_____________________________.
(2)因为∠3+∠4=180°(邻补角的定义),∠3=112°
,所以____________
又因为∠2=68°,
所以___________(等量代换),
所以____∥_________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对下列代数式作出解释,其中不正确的是( )
A. a-b:今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a-b)岁
B. a-b:今年小明b岁,小明的爸爸a岁,则小明出生时,他爸爸为(a-b)岁
C. ab:长方形的长为acm,宽为bcm,长方形的面积为ab ![]()
D. ab:三角形的一边长为acm,这边上的高为bcm,此三角形的面积为ab ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样大小的小正方形纸片,按下图的方式拼正方形:
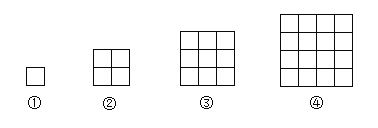
规律:第①个图形中有1个小正方形;
第②个图形比第①个图形多3个小正方形;
第③个图形比第②个图形多5个小正方形;……
第(n+1)个图形比第n个图形多________个小正方形;
可发现以下结论:(1)1+3+5+……+(2n-1)= ____________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖州市在2017年被评为“全国文明城市”,在评选过程中,湖州市环卫处每天需负责市区范围420千米城市道路的清扫工作,现有环卫工人直接清扫和道路清扫车两种马路清扫方式.已知20名环卫工人和1辆道路清扫车每小时可以清扫20千米马路,30名环卫工人和3辆道路清扫车每小时可以清扫42千米的马路.
(1)1名环卫工人和1辆道路清扫车每小时各能清扫多长的马路?
(2)已知2017年环卫处安排了50名环卫工人参与了直接清扫工作,为保证顺利完成每日的420千米清扫工作,需派出多少辆道路清扫车参与工作(已知2017年环卫工人与清扫车每天工作时间为6小时)?
(3)为了巩固文明城市创建成果,从2018年5月开始,环卫处新增了一辆清扫车参与工作,同时又增加了若干个环卫工人参与直接清扫,使得每日能够较早的完成清扫工作。2018年6月市环卫处扩大清扫范围60千米,同时又增加了20名环卫工人直接参与清扫,此时环卫工人和清扫车每日工作时间仍与5月份相同,那么2018年5月环卫处增加了多少名环卫工人参与直接清扫?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解决农民工子女入学难的问题,我市建立了一套进城农民工子女就学的保障机制,其中一项就是免交“借读费”.据统计,2004年秋季有![]() 名农民工子女进入主城区中小学学习,预计2005年秋季进入主城区中小学学习的农民工子女比2004年有所增加,其中小学增加
名农民工子女进入主城区中小学学习,预计2005年秋季进入主城区中小学学习的农民工子女比2004年有所增加,其中小学增加![]() ,中学增加
,中学增加![]() ,这样,2005年秋季将新增
,这样,2005年秋季将新增![]() 名农民工子女在主城区中小学学习.
名农民工子女在主城区中小学学习.
(1)如果按小学每生每年收“借读费”![]() 元,中学每生每年收“借读费”
元,中学每生每年收“借读费”![]() 元计算,求2005年新增加的
元计算,求2005年新增加的![]() 名中小学学生共免收多少“借读费”?
名中小学学生共免收多少“借读费”?
(2)如果小学每增加![]() 名学生需配备
名学生需配备![]() 名教师,中学每增加
名教师,中学每增加![]() 名学生需配备
名学生需配备![]() 名教师,若按2005年秋季入学后,农民工子女在主城区中小学就读的学生增加的人数计算,一共需要配备多少名中小学教师?
名教师,若按2005年秋季入学后,农民工子女在主城区中小学就读的学生增加的人数计算,一共需要配备多少名中小学教师?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( ) 
A.∠ABP=∠C
B.∠APB=∠ABC
C.AB2=AP?AC
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为 ![]() .其中,正确的结论是( )
.其中,正确的结论是( ) 
A.①②④
B.①③⑤
C.②③④
D.①④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com