练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    请根据图中提供的信息,回答下列问题

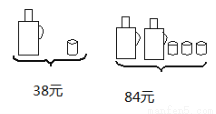
    （1）一个暖瓶与一个水杯分别是多少元?

    （2）甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定： 这两种商品都打九折；乙商场规定：买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯，请问选择哪家商场购买更合算，并说明理由.

    (1)、一个暖瓶30元 一个水杯8元 (2)、乙商场合算 【解析】 试题分析：我们设暖瓶的价格为x元，根据第一个图形可知水杯的价格为(38－x)元，然后根据第二个图形列出方程求出x的值；分求出甲乙两家所需要的费用，然后进行比较. 试题解析：(1)【解析】 设一个暖瓶x元，则一个水杯(38-x)元. 根据题意得2x+3(38-x)=84. 解得x=30. 则38－x=38-...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省武冈市2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    某校数学课外小组利用数轴为学校门口的一条马路设计植树方案如下：第棵树种植在点处，其中，当时， , 表示非负实数的整数部分，例如， ．按此方案，第6棵树种植点为 ________；第2016棵树种植点为_______．

    2 404 【解析】试题解析： …， 当k=6时, 当k=2016时, 故答案为：2，404.

    查看答案和解析>>

    科目：初中数学 来源：江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    从正面观察如图所示的几何体，你所看到的几何体的形状是（ ）

    A. B. C. D.

    A 【解析】试题解析：从正面看，看到的图形是： 故选A.

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：填空题

    将抛物线y=﹣2x2+1向右平移1个单位长度，再向上平移2个单位长度所得的抛物线解析式为___________．

    【解析】试题解析：由“左加右减、上加下减”的原则可知，把抛物线 y=-2x2+1 向右平移 1 个单位，再向 上平移 2 个单位，则平移后的抛物线的表达式为 y=-2（x-1）2+1+2，即 y=-2（x-1）2+3．

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：单选题

    若点B(a，0)在以点A(-1，0)为圆心，2为半径的圆外， 则a的取值范围为（ ）

    A. -3＜a＜1 B. a＜-3 C. a＞1 D. a＜-3或a＞1

    D 【解析】∵点B(a，0)在以点A(-1，0)为圆心，2为半径的圆外， ∴， ∴a＜-3或a＞1. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型：解答题

    先化简，后求值： ，其中x=-2，y=2．

    2x-2y，-8． 【解析】试题分析：先去括号，然后合并同类项，最后代入数值进行计算即可. 试题解析：原式=2x2y+2xy2-2x2y+2x-2xy2-2y=2x-2y， 当x=-2，y=2时，原式=2×（-2）-2×2=-8.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型：填空题

    方程（a-1）x|a|-3=0是关于x的一元一次方程，则a=_______．

    -1 【解析】由题意得： ，解得：a=-1， 故答案为：-1.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型：解答题

    如图，在四边形ABCD中，∠B=90°，AD∥BC，BC=2AD，点E为边BC的中点．

    （1）求证：四边形AECD为平行四边形；

    （2）在CD边上取一点F，联结AF、 AC、 EF，设AC与EF交于点G，且∠EAF=∠CAD．

    求证：△AEC∽△ADF；

    （3）在（2）的条件下，当∠ECA=45°时．求： 的比值．

    （1）证明见解析;（2）证明见解析;（3）． 【解析】试题分析：（1）由E为BC中点，得到BC=2CE，再由BC=2AD，得到AD=CE，再由ADCE，利用一组对边平行且相等的四边形为平行四边形即可得证； （2）由四边形AECD为平行四边形，得到对角相等，再由已知角相等，利用两对角相等的三角形相似即可得证； （3）AD=BE=CE=a,由∠ECA=得到△ABC为等腰直角三角形，即AB=B...

    查看答案和解析>>

    科目：初中数学 来源：北京市延庆区2017-2018学年第一学期八年级期末数学试卷 题型：填空题

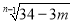    最简二次根式与是同类二次根式，则＝______________．

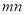    21 【解析】根据二次根式及同类二次根式的定义列出方程组即可求出答案. 【解析】 ∵最简二次根式与是同类二次根式， ∴ ， 解得， ， ∴ 故答案为：21.

    查看答案和解析>>

    同步练习册答案