
【题目】如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是 . (把所有正确结论的序号都填在横线上) ①OG= ![]() AB;
AB;
②与△EGD全等的三角形共有5个;
③S四边形CDGF>S△ABF;
④由点A、B、D、E构成的四边形是菱形.
【答案】①④
【解析】解:∵四边形ABCD是菱形, ∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中, 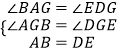 ,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ACD的中位线,
∴OG= ![]() CD=
CD= ![]() AB,①正确;
AB,①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,④正确;
∴AD⊥BE,
由菱形的性质得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中, 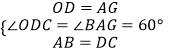 ,
,
∴△ABG≌△DCO(SAS),
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,②不正确;
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG∥AB,OG= ![]() AB,
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∴△GOD的面积= ![]() △ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△AOG的面积=△BOG的面积,
∴S四边形ODGF=S△ABF;不正确;
正确的是①④.
所以答案是:①④.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:初中数学 来源: 题型:
【题目】下列说法不正确的是 ( )
A. 两个单项式的积仍是单项式;
B. 两个单项式的积的次数等于它们的次数之和;
C. 单项式乘以多项式,积的项数与多项式项数相同;
D. 多项式乘以多项式,合并同类项前,积的项数等于两个多项式的项数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△AOB的顶点O在直线l上,且AO=AB.

(1)画出△AOB关于直线l成轴对称的图形△COD,且使点A的对称点为点C ;
(2)在(1)的条件下,AC与BD的位置关系是________;
(3)在(1)、(2)的条件下,联结AD,如果∠ABD=2∠ADB,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为 . 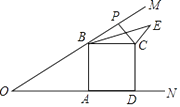
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车油箱内有油48L,从某地出发,每行1km耗油0.6L,如果设剩油量为y(L),行驶路程x(km)写出y与x之间的关系式______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.

(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.阴天一定会下雨
B.购买一张体育彩票,中奖
C.打开电视机,任选一个频道,屏幕上正在播放新闻联播
D.任意画一个三角形,其内角和是180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com