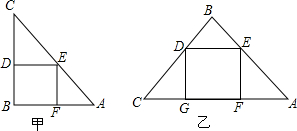Question

1．一块直角三角形木板的直角边BC长为1.5m，AB长为2m．要把它加工成一个面积最大的正方形桌面，甲、乙两位同学的加工方法分别如图所示．请你用学过的知识说明哪位同学的加工方法符合要求．（加工损耗忽略不计）

Answer 1

分析 对于甲图：设正方形的边长为x，则DE=DB=x，CD=1.5-x，证明△CDE∽△CBA，利用相似比可计算出x=$\frac{6}{7}$；对于乙图：作BH⊥ACN，交DE于N，如图乙，先利用勾股定理计算出AC=2.5，再利用面积法计算出BM=1.2，设正方形的边长为y，则DE=DG=y，易得MN=DG=y，则BN=BM-MN=1.2-y，接着证明△BDE∽△BCA，利用相似比可计算出y=$\frac{30}{37}$，然后比较x和y的大小进行判断．

解答 解：对于甲图：设正方形的边长为x，则DE=DB=x，CD=1.5-x，
∵DE∥AB，
∴△CDE∽△CBA，
∴$\frac{DE}{BA}$=$\frac{CD}{CB}$，即$\frac{x}{2}$=$\frac{1.5-x}{1.5}$，解得x=$\frac{6}{7}$，
对于乙图：作BH⊥ACN，交DE于N，如图乙，AC=$\sqrt{1．{5}^{2}+{2}^{2}}$=2.5，
∵$\frac{1}{2}$BM•AC=$\frac{1}{2}$BC•BA，
∴BM=$\frac{1.5×2}{2.5}$=1.2，
设正方形的边长为y，则DE=DG=y，
易得四边形DGMN为矩形，
∴MN=DG=y，
∴BN=BM-MN=1.2-y，
∵DE∥AC，
∴△BDE∽△BCA，
∴$\frac{BN}{BM}$=$\frac{DE}{CA}$，即$\frac{1.2-y}{1.2}$=$\frac{y}{2.5}$，解得y=$\frac{30}{37}$，
∵x=$\frac{6}{7}$=$\frac{30}{35}$＞$\frac{30}{37}$=y，
∴甲图中的正方形的面积要大，
所以甲同学的加工方法符合要求．

点评 本题考查了相似三角形的应用：常常构造“A”型或“X”型相似图，然后利用三角形相似的性质计算相应线段的长．也考查了正方形的性质．