练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正方形的对角线，相交于点．

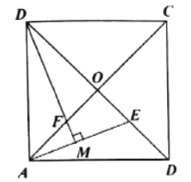
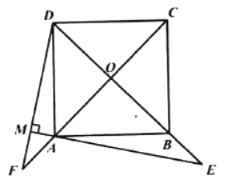
    （1） （2）

    （1）若点是上一点，连接，过点作，垂足为，与相交于点．求证：；

    （2）若点在的延长线上，于点，交的延长线于点，其他条件不变结论“”还成立吗？如果成立，请给出证明；如果不成立，请说明理由．

    【答案】（1）证明见解析；（2）“OE = OF”仍然成立；理由见解析．

    【解析】

    （1）由四边形ABCD为平行四边形，得到对角线垂直且互相平分，再由DM与AE垂直，得到一组对角相等，进而得到≌，利用全等三角形对应边相等即可得证；

    （2）其他条件不变．结论“OE=OF”还成立，理由为：同（1）得到全等三角形，即可得证．

    （1）证明：∵正方形ABCD的对角线AC，BD相交于点O，

    ∴，．

    ∴

    ∵，，

    ∴．

    ∴≌．

    ∴．

    （2）结论：“OE = OF”仍然成立

    证明：∵正方形ABCD的对角线AC，BD相交于点O，

    ∴，．

    ∴．

    ∵，，

    ∴．

    ∴≌．

    ∴．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，反比例函数（k＜0）的图象经过点A（-1，1），过点A作AB⊥y轴，垂足为B，在y轴的正半轴上取一点P（0，t），过点P作直线OA的垂线l，以直线l为对称轴，点B经轴对称变换得到了点B’在此反比例函数的图象上，则t的值是（ ）

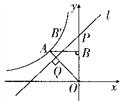
    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂现在平均每天比原计划多生产 50 台机器，现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同．

    （1）现在平均每天生产多少台机器；

    （2）生产 3000 台机器，现在比原计划提前几天完成．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“2018东台西溪半程马拉松”的赛事共有两项：A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作， 组委会随机将志愿者分配到两个项目组．

    （1）小明被分配到“半程马拉松”项目组的概率为________．

    （2）为估算本次赛事参加“半程马拉松”的人数，小明对部分参赛选手作如下调查：

    调查总人数

    20

    50

    100

    200

    500

    参加“半程马拉松”人数

    15

    33

    72

    139

    356

    参加“半程马拉松”频率

    0.750

    0.660

    0.720

    0.695

    0.712

    ①请估算本次赛事参加“半程马拉松”人数的概率为_______．（精确到0.1）

    ②若本次参赛选手大约有3000人，请你估计参加“半程马拉松”的人数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情境：在等腰直角三角形ABC中，， 直线过点且，过点为一锐角顶点作，且点在直线上（不与点重合），如图1， 与交于点，试判断与的数量关系，并说明理由．探究展示：小星同学展示出如下正确的解法：

    解：，证明如下：

    过点作，交于点

    则为等腰直角三角形

    （依据）

    在与中

    （依据）

    （1）反思交流：上述证明过程中的“依据”和“依据”分别是指：

    依据：

    依据：

    拓展延伸：（2）在图2中，与延长线交于点，试判断与的数量关系，并写出证明过程

    （3）在图3中，与延长线交于点，试判断与的数量关系，并写出证明过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】元旦期间，某商场为了吸引顾客，开展有奖促销活动，设立了一个可以自由转动的转盘，转盘被分成4个面积相等的扇形，四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样（如图）．规定：同一日内，顾客在本商场每消费满100元就可以转动转盘一次，商场根据转盘指针指向区域所标金额返还相应数额的购物券，某顾客当天消费240元，转了两次转盘．

    （1）该顾客最少可得_________元购物券，最多可得_________元购物券；

    （2）请用画树状图或列表的方法，求该顾客所获购物券金额不低于50元的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数和．

    （1）在同一直角坐标系内，画出这两个函数的大致图象；

    （2）直接写出：①函数与坐标轴围成的图形的面积为_______；

    ②函数与坐标轴围成的图形的面积为________；

    ③这两个函数图象与轴围成的图形的面积为_________．

    （3）若反比例函数经过这两个函数图象的交点，则k的值为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，点， 在反比例函数（m为常数）的图象上，连接AO并延长与图象的另一支有另一个交点为点C，过点A的直线l与x轴的交点为点，过点C作CE∥x轴交直线l于点E．

    （1）求m的值，并求直线l对应的函数解析式；

    （2）求点E的坐标；

    （3）过点B作射线BN∥x轴，与AE交于点M (补全图形)，求证：

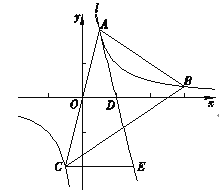
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD的对角线相交于点O，延长AB至点E，使BE＝AB，连接CE，∠E＝50°．

    （1）求证：BD＝EC；

    （2）求∠BAO的大小．

    查看答案和解析>>

    同步练习册答案