
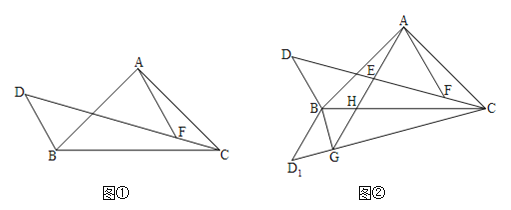
【题目】已知△ABC,AB=AC,∠BAC=90°,D为△ABC外部一点,∠BDC=45°,点F在CD上且AF∥DB.
(1)如图①,求证:![]() ;
;
(2)如图②,将△BCD沿BC翻折得到△BCD1,过点B作BG⊥CD1,垂足为G,连接AG交CD于E,交BC于H.若AF=![]() ,∠BCD=15°,求AG的长度.
,∠BCD=15°,求AG的长度.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)过点A作AM⊥AF,交DC于点M,连接BM,利用平行线的性质得到∠AMF=45°,从而得到△AMF是等腰直角三角形,MF=![]() ,然后利用AAS定理证得△ABM≌△ACF,然后根据全等三角形的性质得出∠AMB=∠AFC=180°-∠AFM=135°,再结合已知条件求得△BDM是等腰直角三角形,
,然后利用AAS定理证得△ABM≌△ACF,然后根据全等三角形的性质得出∠AMB=∠AFC=180°-∠AFM=135°,再结合已知条件求得△BDM是等腰直角三角形,![]() ,从而使问题得解;
,从而使问题得解;
(2)过点A作AM⊥AF,交DC于点M,连接BM,过点A作AN⊥CD,AK⊥CG,根据(1)中的证明,通过利用等腰直角三角形及折叠的性质得到CD=C D1=![]() ,∠D=∠D1=45°,∠DCB=∠D1CB=15°,BC平分∠DCD1,然后利用含30°直角三角形的性质,求得
,∠D=∠D1=45°,∠DCB=∠D1CB=15°,BC平分∠DCD1,然后利用含30°直角三角形的性质,求得![]() ,
,![]() ,最后利用勾股定理求解.
,最后利用勾股定理求解.
解:(1)如图1,过点A作AM⊥AF,交DC于点M,连接BM
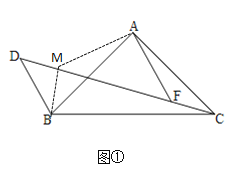
∵∠BDC=45°,且AF∥DB
∴∠AFM=45°
又∵AM⊥AF,∴∠MAF=90°
∴∠AMF=∠AFM=45°
∴AM=AF,即△AMF是等腰直角三角形
∴MF=![]()
又因为∠BAC=90°,∠MAF=90°
∴∠MAB+∠BAF=∠FAC+∠BAF=90°
∴∠MAB =∠FAC
又∵AB=AC
∴△ABM≌△ACF
∴∠AMB=∠AFC=180°-∠AFM=135°
所以∠BMC=90°
又因为∠BDC=45°
∴△BDM是等腰直角三角形
∴![]()
∴DF-MF=DM
即![]() ;
;
(2)如图2,过点A作AM⊥AF,交DC于点M,连接BM,过点A作AN⊥CD,AK⊥CG
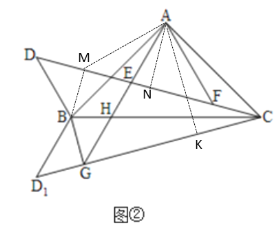
由(1)可知△BDM和△AMF是等腰直角三角形, △ABM≌△ACF
∴AM=AF=![]() ,MF=
,MF=![]() ,∠AMF=45°
,∠AMF=45°
又∵AN⊥CD
∴![]()
∵∠BCD=15°,∴在Rt△ANC中,∠CAN=30°
∴AC=2AN=2,CN=![]()
又∵等腰直角△AMF中,AN⊥MF,
∴MN=NF
∵△ABM≌△ACF且△BDM是等腰直角三角形
∴BM=DM=CF
∴MN+DM=NF+CF
∴CD=![]() ,DM=BM=CF=
,DM=BM=CF=![]()
又由折叠性质可知,CD=C D1=![]() ,∠D=∠D1=45°,∠DCB=∠D1CB=15°,BC平分∠DCD1
,∠D=∠D1=45°,∠DCB=∠D1CB=15°,BC平分∠DCD1
∴∠ACK=60°,在Rt△ACK中,∠CAK=30°
∴![]() ,
,![]()
∵BG⊥CD1,BM⊥CD
∴BG=D1G=![]() ,CG=
,CG=![]()
∴GK=CG-CK=![]()
∴在Rt△AGK中,![]() .
.


科目:初中数学 来源: 题型:
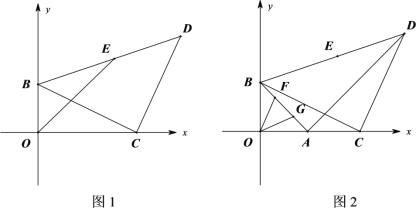
【题目】在平面直角坐标系xOy中,A(a,0),B(0,b)其中a,b满足![]() .点C为x轴正半轴上的一点,且点C在点A右侧,若点D为第一象限内一点,且满足CD⊥CB,
.点C为x轴正半轴上的一点,且点C在点A右侧,若点D为第一象限内一点,且满足CD⊥CB,![]() .
.
(1)求A,B的坐标;
(2)如图1,点E为BD中点,连接OE,求证:![]() ;
;
(3)如图2,若点F、G是BA上的两个动点,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
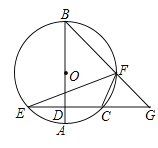
【题目】如图,AB为⊙O的直径,C,F为⊙O上两点,过C作CD⊥AB于点D,交⊙O于点E,延长EC交BF的延长线于点G,连接CF,EG.
(1)求证:∠BFE=∠CFG;
(2)若FG=4,BF=6,CF=3.求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,命题:①若∠B=∠C-∠A,则△ABC是直角三角形.②若a2=(b+c)(b-c),则△ABC是直角三角形.③若∠A∶∠B∶∠C=3∶4∶5,则△ABC是直角三角形.④若a∶b∶c=5∶4∶3.则△ABC是直角三角形. 其中假命题个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距300千米,甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留1小时后,速度不变,按原路返回.设两车行驶的时间是x小时,离开A地的距离是y千米,如图是y与x的函数图象.
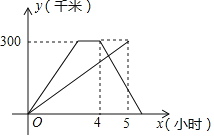
(1)甲车的速度是 ,乙车的速度是 ;
(2)甲车在返程途中,两车相距20千米时,求乙车行驶的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,AB的垂直平分线交线段AC于D,若△ABC和△DBC的周长分别是60 cm和38 cm,则△ABC的腰长和底边BC的长分别是( )
A. 22cm和16cmB. 16cm和22cm
C. 20cm和16cmD. 24cm和12cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com