
【题目】对于下列结论: ①二次函数y=6x2 , 当x>0时,y随x的增大而增大.
②关于x的方程a(x+m)2+b=0的解是x1=﹣2,x2=1(a、m、b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是x1=﹣4,x2=﹣1.
③设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是c≥3.
其中,正确结论的个数是( )
A.0个
B.1个
C.2个
D.3个
【答案】D
【解析】解:①∵在二次函数y=6x2中,a=6>0,b=0, ∴抛物线的对称轴为y轴,当x>0时,y随x的增大而增大,
∴①结论正确;
②∵关于x的方程a(x+m)2+b=0的解是x1=﹣2,x2=1,
∴x+m=﹣2+m或1+m,
∴方程a(x+m+2)2+b=0中,
x+m+2=﹣2+m或x+m+2=1+m,
解得:x1=﹣4,x2=﹣1,
∴②结论正确;
③∵二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,
∴  ,
,
解得:b≤﹣4,c≥3,
∴结论③正确.
故选D.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】为支持四川抗震救灾,重庆市A、B、C三地现在分别有赈灾物资100吨、100吨、80吨,需要全部运往四川重灾地区的D、E两县.根据灾区的情况,这批赈灾物资运往D县的数量比运往E县的数量的2倍少20吨.
(1)求这批赈灾物资运往D、E两县的数量各是多少?
(2)若要求C地运往D县的赈灾物资为60吨,A地运往D的赈灾物资为x吨(x为整数),B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍.其余的赈灾物资全部运往E县,且B地运往E县的赈灾物资数量不超过25吨.则A、B两地的赈灾物资运往D、E两县的方案有几种?请你写出具体的运送方案;
(3)已知A、B、C三地的赈灾物资运往D、E两县的费用如下表:
A地 | B地 | C地 | |
运往D县的费用(元/吨) | 220 | 200 | 200 |
运往E县的费用(元/吨) | 250 | 220 | 210 |
为及时将这批赈灾物资运往D、E两县,某公司主动承担运送这批赈灾物资的总费用,在(2)问的要求下,该公司承担运送这批赈灾物资的总费用最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:3+2=3×2﹣1,4+![]() =4×
=4×![]() ﹣1,给出定义如下:
﹣1,给出定义如下:
我们称使等式a+b=ab﹣1成立的一对有理数a,b为“椒江有理数对”,记为(a,b),如:数对(3,2),(4,![]() )都是“椒江有理数对”.
)都是“椒江有理数对”.
(1)数对(﹣2,1),(5,![]() )中是“椒江有理数对”的是 ;
)中是“椒江有理数对”的是 ;
(2)若(a,3)是“椒江有理数对”,求a的值;
(3)若(m,n)是“椒江有理数对”,则(﹣n,﹣m) “椒江有理数对”(填“是”、“不是”或“不确定”).
(4)请再写出一对符合条件的“椒江有理数对”
(注意:不能与题目中已有的“椒江有理数对”重复)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校从初二(1)班和(2)班各选拔10名同学组成甲队和乙队,参加数学竞赛活动,此次竞赛共有10道选择题,答对8题(含8题)以上为优秀,两队选手答对题数统计如下:
答对题数 | 5 | 6 | 7 | 8 | 9 | 10 | 平均数( |
甲队选手 | 1 | 0 | 1 | 5 | 2 | 1 | 8 |
乙队选手 | 0 | 0 | 4 | 3 | 2 | 1 | a |
中位数 | 众数 | 方差(s2) | 优秀率 | ||||
甲队选手 | 8 | 8 | 1.6 | 80% | |||
乙队选手 | b | c | 1.0 | m | |||
(1)上述表格中,a= ,b= ,c= ,m= .
(2)请根据平均数和众数的意义,对甲、乙两队选手进行评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10 ![]() 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为海里/小时?
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为海里/小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N. 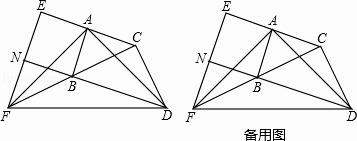
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD= ![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中. 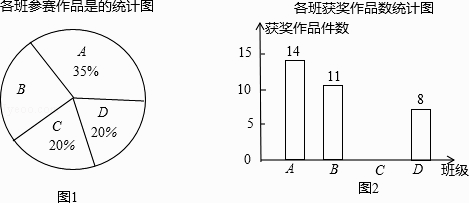
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放入箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com