
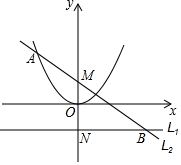
 已知a>0,直线L1:y=-$\frac{1}{4a}$与y轴交于点N,点N关于原点的对称点为点M,过点M的直线L2与抛物线y=ax2在第二象限交于点A,与直线L1交于点B,且MA=MB,平移直线L2,使之与抛物线有唯一公共点,且与y轴交于点P.求证:$\frac{OM}{OP}$为一定值.
已知a>0,直线L1:y=-$\frac{1}{4a}$与y轴交于点N,点N关于原点的对称点为点M,过点M的直线L2与抛物线y=ax2在第二象限交于点A,与直线L1交于点B,且MA=MB,平移直线L2,使之与抛物线有唯一公共点,且与y轴交于点P.求证:$\frac{OM}{OP}$为一定值. 分析 既然要证明OM与OP的比值为定值,那么只需分别表示出两条线段的长度,然后作商即可.易求N、M的坐标,从而求得MN的长度,由于M是AB中点,于是考虑作AH垂直BN于H,则AH的长度是MN的2倍,进而求出A的纵坐标,代入抛物线解析式求得A的坐标,接着可得出直线AB的解析式,平移后的直线与AB是平行的,因此只需设出平移后的直线的截距,然后将平移后的直线解析式与抛物线的解析式联立方程组,利用判别式为0得出截距,即可得出P点坐标,接着即可算出OM与OP的长度,两者相比必为常数.
解答 证明:∵y=-$\frac{1}{4a}$与y轴交于点N,
∴N(0,-$\frac{1}{4a}$),
∵点N关于原点的对称点为点M,
∴M(0,$\frac{1}{4a}$),
∴MN=$\frac{1}{2a}$,
过点A作AH⊥BN于H,如图,
∵MA=MB,
∴AH=2MN=$\frac{1}{a}$,
∴A点的纵坐标为$\frac{1}{a}-\frac{1}{4a}=\frac{3}{4a}$,
∵A点在抛物线y=ax2上,且在第二象限,
∴A($-\frac{\sqrt{3}}{2a}$,$\frac{3}{4a}$),
∴B($\frac{\sqrt{3}}{2a}$,$-\frac{1}{4a}$),
∴直线AB的解析式为:$y=-\frac{\sqrt{3}}{3}x+\frac{1}{4a}$,
设将AB平移到与抛物线有唯一公共点时对应的直线解析式为:$y=-\frac{\sqrt{3}}{3}x+b$,
联立方程组$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x+b}\\{y=a{x}^{2}}\end{array}\right.$,消去y整理得:$3a{x}^{2}+\sqrt{3}x-3b=0$,
∴△=3+36ab=0,
∴$b=-\frac{1}{12a}$,
∴P(0,-$\frac{1}{12a}$),
∴OP=$\frac{1}{12a}$,OM=$\frac{1}{4a}$,
∴$\frac{OM}{OP}=3$(定值).
点评 本题主要考查了二次函数的性质、坐标点的对称,中位线、待定系数法求一次函数解析式,直线的平移,二元二次方程组,一元二次方程根的判别式等知知识点,题虽小,综合性却很强,有一定难度.求得AB的解析式进而求出P点坐标是解决本题的关键所在.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:解答题
| 甲 | 160 | 173 | 172 | 161 | 162 | 171 | 170 | 175 |
| 乙 | 170 | 165 | 168 | 169 | 172 | 173 | 168 | 167 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
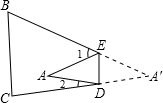 如图所示,把纸片△A′BC沿DE折叠,点A′落在四边形BCDE内部点A处.
如图所示,把纸片△A′BC沿DE折叠,点A′落在四边形BCDE内部点A处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
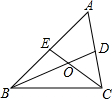 已知:如图,△ABC的中线BD、CE交于点O.
已知:如图,△ABC的中线BD、CE交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com