
 正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.
正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.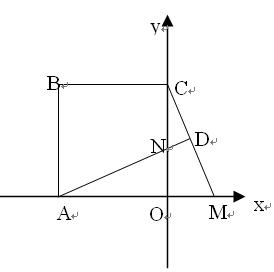
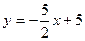 …………(2分)
…………(2分) 2)S=
2)S=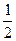 t2+
t2+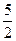 t(t>0)……(1分) t=1……(1分)
t(t>0)……(1分) t=1……(1分) 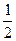 t2-
t2-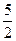 t(-5<t<0)…(1分) t=-2,t=-3 (1分)
t(-5<t<0)…(1分) t=-2,t=-3 (1分)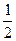 t2+
t2+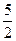 t(t<-5)……(1分) t=-6……(1分)
t(t<-5)……(1分) t=-6……(1分)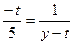 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
 中,抛物线
中,抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左边),与
的左边),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
. 的值;
的值; 上是否存在点
上是否存在点 ,使
,使 与
与 相似.若存在,求出点
相似.若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
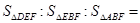 ( ▲ )
( ▲ )| A.1:3:9 | B.1:5:9 | C.2:3:5 | D.2:3:9 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.2:1 | B.1:2 |
| C.4:1 | D.1:4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
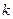 ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?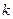 = 1时,是 ;
= 1时,是 ;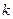 = 2时,是 ;
= 2时,是 ;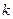 = 3时,是 .
= 3时,是 .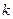 = 2时的结论.
= 2时的结论.

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.
,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.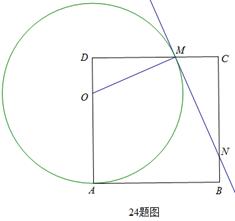
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
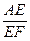 的值.
的值. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

| OE |
| DC |
| 1 |
| 2 |
| EF |
| FD |
| OE |
| DC |
| 1 |
| 2 |
| EF |
| ED |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com