
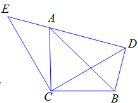
【题目】如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CD=CE,△ACB的顶点A在△ECD的斜边DE上,连接BD.

(1)求证:BD=AE;
(2)若AE=5cm,AD=7cm,求AC的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据同角的余角相等得出∠BCD=∠ACE,然后根据SAS定理证明△BCD≌△ACE,从而得出结论;
(2)根据全等三角形的性质得出∠BDC=∠AEC,然后结合等腰直角三角形的性质求得∠BDA是直角三角形,从而利用勾股定理求解.
(1)∵△ACB和△ECD都是等腰直角三角形
∴∠ACB=∠ECD=90°
∴∠ACD+∠BCD=90°,∠ACD+∠ACE=90°
∴∠BCD=∠ACE
在△BCD和△ACE中
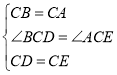
∴△BCD≌△ACE(SAS)
∴BD=AE
(2)∵△BCD≌△ACE
∴∠BDC=∠AEC
又∵△ECD是等腰直角三角形
∴∠CDE=∠CED=45°
∴∠BDC=45°
∴∠BDC+∠CDE=90°
∴∠BDA是直角三角形
∴![]()
在等腰直角三角形ACB中
![]()
∴![]()


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
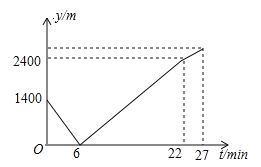
【题目】(2017湖北省鄂州市,第8题,3分)小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,图中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家的速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应数值:
的几组对应数值:
| … |
|
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| 0 |
|
|
|
| 2 |
|
| … |
①写出![]() 的值为 ;
的值为 ;
②在平面直角坐标系中,描出了以表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
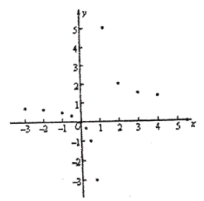
(3)当![]() 时,直接写出x的取值范围为: .
时,直接写出x的取值范围为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过A(-1,0)、B(4,5)三点.
的图象经过A(-1,0)、B(4,5)三点.
(1)求此二次函数的解析式;
(2)当x为何值时,y随x的增大而减小?
(3)当x为何值时,y>0?
查看答案和解析>>
科目:初中数学 来源: 题型:
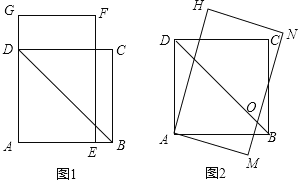
【题目】如图1,四边形ABCD是边长为![]() 的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
(1)求∠DOM的度数;
(2)图2中,求D、N两点间的距离;
(3)若将矩形AMNH绕点A再顺时针旋转15°得到矩形APQR,此时点B在矩形APQR的内部、外部还是边上?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于关于x的二次函数y=x2-2mx-3,有下列说法:① 它的图象与x轴有两个公共点; ② 如果当x≤1时y随x的增大而减小,则m=1; ③ 如果将它的图象向左平移3个单位后过原点,则m=-1; ④ 如果当x=5时的函数值与x=2012时的函数值相等,则当x=2017时的函数值为-3.其中正确的说法有______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为4元/件的日用品。若按每件5元的价格出售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件;假定每月的销售件数y(万件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x的函数关系式;
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年巴西里约奥运会期间,南京某奥运特许经营商店以每件
年巴西里约奥运会期间,南京某奥运特许经营商店以每件![]() 元的价格购进了一批奥运纪念
元的价格购进了一批奥运纪念![]() 恤,定价为
恤,定价为![]() 元时,平均每天可售出
元时,平均每天可售出![]() 件,为了扩大销售,增加盈利,此奥运特许经营商店决定采取适当的降价措施,经调查发现,在一定范围内,奥运纪念
件,为了扩大销售,增加盈利,此奥运特许经营商店决定采取适当的降价措施,经调查发现,在一定范围内,奥运纪念![]() 恤的单价每降
恤的单价每降![]() 元,每天可多售出
元,每天可多售出![]() 件.当这种奥运纪念
件.当这种奥运纪念![]() 恤每件的价格定为多少元时,商店每天获利
恤每件的价格定为多少元时,商店每天获利![]() 元?
元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com