练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】平行四边形中，、是对角线上不同的两点，下列条件中，不能得到四边形一定为平行四边形的是（ ）

    A.B.C.D.

    【答案】C

    【解析】

    连接AC与BD相交于O，根据平行四边形的对角线互相平分可得OA=OC，OB=OD，再根据对角线互相平分的四边形是平行四边形，只要证明得到OE=OF即可，然后根据各选项的条件分析判断即可得解．

    如图，连接AC与BD相交于O，


    在ABCD中，OA=OC，OB=OD，
    要使四边形AECF为平行四边形，只需证明得到OE=OF即可；
    A、若BE=DF，则OB-BE=OD-DF，即OE=OF，故本选项不符合题意；
    B、AF∥CE能够利用“角角边”证明△AOF和△COE全等，从而得到OE=OF，故本选项不符合题意；
    C、若AE=CF，则无法判断OE=OE，故本选项符合题意；
    D、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等，从而得到DF=BE，然后同A，故本选项不符合题意；
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图（a），将两块直角三角尺的直角顶点C叠放在一起．

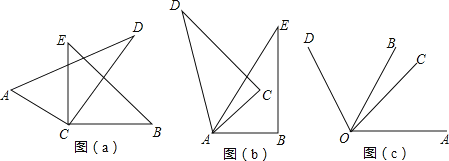
    （1）若∠DCE＝35°，∠ACB＝　 　；若∠ACB＝140°，则∠DCE＝　 　；并猜想∠ACB与∠DCE的大小有何特殊关系，并说明理由；

    （2）如图（b），若是两个同样的三角尺60°锐角的顶点A重合在一起，则∠DAB与∠CAE的大小有何关系，请说明理由；

    （3）已知∠AOB＝α，∠COD＝β（都是锐角），如图（c），若把它们的顶点O重合在一起，请直接写出∠AOD与∠BOC的大小相等的关系（用含有α，β的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数的图象经过点，与轴分别交于点，点.点是直线上方的抛物线上一动点.

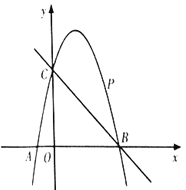
    （1）求二次函数的表达式；

    （2）连接，，并把沿轴翻折，得到四边形.若四边形为菱形，请求出此时点的坐标；

    （3）当点运动到什么位置时，四边形的面积最大？求出此时点的坐标和四边形的最大面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线（a≠0）的图象与x轴交于A、B两点，与y轴交于C点，已知B点坐标为（4，0）．

    （1）求抛物线的解析式；

    （2）试探究△ABC的外接圆的圆心位置，并求出圆心坐标；

    （3）若点M是线段BC下方的抛物线上一点，求△MBC的面积的最大值，并求出此时M点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB＝AC＝2，BC边上有10个不同的点P1，P2，……，P10， 记（i ＝ 1，2，……，10），那么 M1+M2+……+M10的值为（ ）

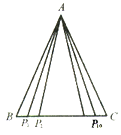
    A. 4 B. 14 C. 40 D. 不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图 ，在中， ，，点、为 边上两点， 将、分别沿、折叠，、两点重合于点，若，则的长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）水果店张阿姨以每斤2元的价格购进某种水果若干斤，然后以每斤4元的价格出售，每天可售出100斤，通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出20斤，为保证每天至少售出260斤，张阿姨决定降价销售．

    （1）若将这种水果每斤的售价降低x元，则每天的销售量是 斤（用含x的代数式表示）；

    （2）销售这种水果要想每天盈利300元，张阿姨需将每斤的售价降低多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

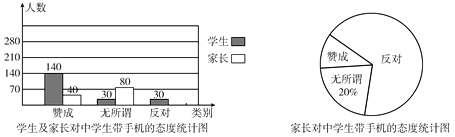
    【题目】“校园手机”现象越来越受到社会的关注，“六一”期间，记者随机调查了某校若干名初四学生和家长对中学生带手机现象的看法，统计整理并制作了如下两幅统计图.

    （1）求这次调查的家长人数，并补全条形图；

    （2）求扇形图中表示家长“赞成”的圆心角的度数；

    （3）若南岗区共有初四学生10000名，请估计在这些学生中，对中学生带手机现象持“无所谓”态度的人数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)我国著名的数学家赵爽，早在公元3世纪，就把一个矩形分成四个全等的直角三角形，用四个全等的直角三角形拼成丁一个大的正方形（如图1），这个矩形称为赵爽弦图，验证了一个非常重要的结论：在直角三角形中两直角边a、b与斜边c满足关系式a2＋b2＝c2，称为勾股定理.

    证明：∵大正方形面积表示为S＝c2，，又可表示为S＝4×ab＋(b－a)2，

    ∴4×ab＋(b－a)2＝c2.

    ∴______________

    即直角三角形两直角边的平方和等于斜边的平方.

    (2)爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图2)，也能验证这个结论，请你帮助小明完成验证的过程.

    (3)如图3所示，∠ABC＝∠ACE＝90°，请你添加适当的辅助线，证明结论a2＋b2＝c2.

    查看答案和解析>>

    同步练习册答案