
分析 根据二次项系数非0,以及b2-4ac>0,可得出关于k的一元二次不等式组,解不等式组即可得出k的取值范围,结合k为偶数即可得出结论.
解答 解:由已知得:$\left\{\begin{array}{l}{(k-2)^{2}≠0}\\{(2k+1)^{2}-4(k-2)^{2}>0}\end{array}\right.$,
解得:k>$\frac{3}{4}$且k≠2,
∵k为偶数,
∴k的最小值为4.
故答案为:4.
点评 本题考查了根的判别式以及解一元二次不等式组,解题的关键根据已知得出不等式组.本题属于基础题,难度不大,解决该题型题目时,由根的判别式以及二次项系数非0得出不等式(或不等式组)是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r=$\sqrt{2}$时,S为$\frac{π}{2}$-1.
如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r=$\sqrt{2}$时,S为$\frac{π}{2}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 68.77×109 | B. | 6.877×109 | C. | 6.877×1010 | D. | 6877×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
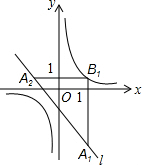 如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2=-$\frac{3}{2}$,a2016=-$\frac{1}{3}$;若要将上述操作无限次地进行下去,则a1不可能取的值是0或-1.
如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2=-$\frac{3}{2}$,a2016=-$\frac{1}{3}$;若要将上述操作无限次地进行下去,则a1不可能取的值是0或-1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,点E在BC上,AE交BD于点F,如果$\frac{BE}{CE}$=$\frac{3}{2}$,那么$\frac{BF}{DF}$=$\frac{3}{5}$.
如图,在?ABCD中,点E在BC上,AE交BD于点F,如果$\frac{BE}{CE}$=$\frac{3}{2}$,那么$\frac{BF}{DF}$=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com