
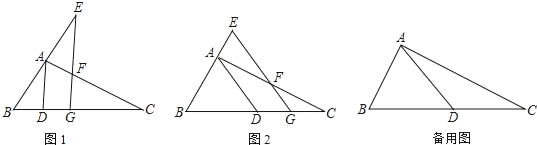
【题目】如图,Rt△ABC中,∠BAC=90°,AB=2,AC=4,D是BC边上一动点,G是BC边上的一动点,GE∥AD分别交AC、BA或其延长线于F、E两点
(1)如图1,当BC=5BD时,求证:EG⊥BC;
(2)如图2,当BD=CD时,FG+EG是否发生变化?证明你的结论;
(3)当BD=CD,FG=2EF时,DG的值= .
【答案】(1)证明见解析;(2)不变;EG+FG=2![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)利用勾股定理得出BC,进一步得出BD,之后证明△BDA∽△BAC,所以∠BDA=∠BAC=90°,根据GE∥AD进一步得出结论即可;
(2)当BD=CD时,FG+EG不发生变化,且FG+EG=![]() ,利用△CFG∽△CAD进一步证明即可得出结论;
,利用△CFG∽△CAD进一步证明即可得出结论;
(3)分两种情况:当F在CA的延长线上和E在BA的延长线上,据此分别画出图形,利用相似得出答案即可.
证明:(1)如图1,

∵∠BAC=90°,AB=2,AC=4,
∴BC=2![]() ,
,
∵BC=5BD,
∴BD=![]() ,
,
∴![]() ,
,
又∵∠DBA=∠ABC,
∴△BDA∽△BAC,
∴∠BDA=∠BAC=90°,
∵EG∥AD,
∴EG⊥BC.
(2)FG=EG=2![]() 不变,
不变,
如图2,

∵EG∥AD,
∴△CFG∽△CAD,
∴![]() ,
,
同理![]() ,
,
∵BD=CD,
∴![]() +
+![]() =
=![]() +
+![]() =2,
=2,
∴EG+FG=2AD,
∵BD=CD,∠BAC=90°,
∴AD=![]() BC=
BC=![]() ,
,
∴EG+FG=2AD=2![]() .
.
(3)如图,

当BD=CD,FG=2EF时,
则GE=EF,
∵GE∥AD,AD∥GF,
∴△CFG∽△CAD,△ABD∽△BGE,
∴![]() ,
,![]() ,
,
∴![]() =
=![]() ,
,
又BG+CG=2![]() ,
,
∴BG=![]() ,
,
∴DG=BD=BG=![]() ;
;
如图,

当BD=CD,FG=2EF时,
则GE=EF,
∵GE∥AD,AD∥GF,
∴△CFG∽△CAD,△ABD∽△AGE,
∴![]() ,
,![]() ,
,
∴![]() =
=![]() ,
,
又BG+CG=2![]() ,
,
∴CG=![]() ,
,
∴DG=CD﹣CG=![]() .
.
综上所知DG为![]() 或
或![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与反比例函数的图象交于A(﹣2,1),B(1,n)两点.
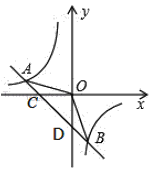
根据以往所学的函数知识以及本题的条件,你能提出求解什么问题?并解决这些问题(至少三个问题).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月31日是第31个“世界无烟日”,校学生会书记小明同学就“戒烟方式”的了解程度对本校九年级学生进行了一次随机问卷调查,下图是他采集数据后绘制的两幅不完整的统计图(A:了解较多,B:不了解,C:了解一点,D:非常了解).请你根据图中提供的信息解答以下问题:
(1)在扇形统计图中的横线上填写缺失的数据,并把条形统计图补充完整.
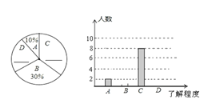
(2)2018年该初中九年级共有学生400人,按此调查,可以估计2018年该初中九年级学生中对戒烟方式“了解较多”以上的学生约有多少人?
(3)在问卷调查中,选择“A”的是1名男生,1名女生,选择“D”的有2名女生.校学生会要从选择“A、D”的问卷中,分别抽一名学生参加活动,请你用列表法或树状图求出恰好是一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量![]() 与时间第
与时间第![]() 天之间的函数关系式为
天之间的函数关系式为![]() (
(![]() ,
,![]() 为整数),销售单价
为整数),销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间满足一次函数关系如下表:
天之间满足一次函数关系如下表:
时间第 | 1 | 2 | 3 | … | 80 |
销售单价 | 49. 5 | 49 | 48. 5 | … | 10 |
(1)写出销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )

A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合实践:
问题情境
数学活动课上,老师和同学们在正方形中利用旋转变换探究线段之间的关系探究过程如下所示:如图I,在正方形![]() 中,点
中,点![]() 为边
为边![]() 的中点.将
的中点.将![]() 以点
以点![]() 为旋转中心,顺时针方向旋转,当点
为旋转中心,顺时针方向旋转,当点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上时,连接
上时,连接![]() .
.

“兴趣小组”发现的结论是:![]() ;
;
“卓越小组”发现的结论是:![]() .
.
解决问题
(1)请你证明“兴趣小组”和“卓越小组”发现的结论;
拓展探究
证明完“兴趣小组”和“卓越小组”发现的结论后,“智慧小组”提出如下问题:如图2,连接![]() ,若正方形
,若正方形![]() 的边长为
的边长为![]() ,求出
,求出![]() 的长度.
的长度.
(2)请你帮助智慧小组写出线段![]() 的长度.(直接写出结论即可)
的长度.(直接写出结论即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表所示.现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中不正确的是( )
操作组 | 管理组 | 研发组 | |
日工资(元/人) | 260 | 280 | 300 |
人数(人) | 4 | 4 | 4 |
A.团队平均日工资不变B.团队日工资的方差不变
C.团队日工资的中位数不变D.团队日工资的极差不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图二次函数![]() 的图像交
的图像交![]() 轴于
轴于![]() 、
、![]() ,交
,交![]() 轴于
轴于![]() ,直线
,直线![]() 平行于
平行于![]() 周,与抛物线另一个交点为
周,与抛物线另一个交点为![]() .
.
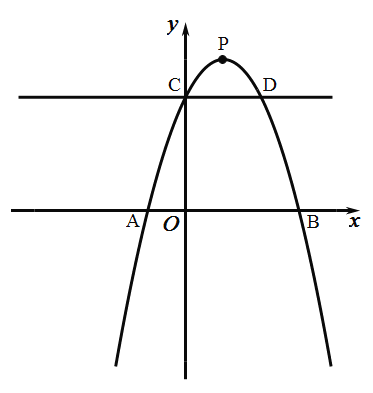
(1)求函数的解析式;
(2)若![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 是抛物线上的动点,求使以
是抛物线上的动点,求使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形的
为顶点的四边形是平行四边形的![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
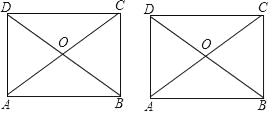
【题目】如图,已知矩形ABCD,AB=6,AD=2![]() ,对角线AC,BD交于点O,E为对角线AC上一点.
,对角线AC,BD交于点O,E为对角线AC上一点.
(1)求证:△OBC是等边三角形;
(2)连结BE,当BE=![]() 时,求线段AE的长;
时,求线段AE的长;
(3)在BC边上取点F,设P,Q分别为线段AE,BF的中点,连结EF,PQ.若EF=2,求PQ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com