
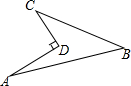
 如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.
如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.| A. | 96 | B. | 204 | C. | 196 | D. | 304 |
分析 连接AC,先利用勾股定理求出AC,再根据勾股定理的逆定理判定△ABC是直角三角形,那么△ABC的面积减去△ACD的面积就是所求的面积.
解答 解:如图,连接AC.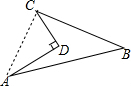
在△ACD中,∵AD=12m,CD=9m,∠ADC=90°,
∴AC=15m,
又∵AC2+BC2=152+202=252=AB2,
∴△ABC是直角三角形,
∴这块地的面积=△ABC的面积-△ACD的面积=$\frac{1}{2}$×15×20-$\frac{1}{2}$×9×12=96(平方米).
故选A.
点评 本题考查了勾股定理、勾股定理的逆定理的应用,得到△ABC是直角三角形是解题的关键.同时考查了直角三角形的面积公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
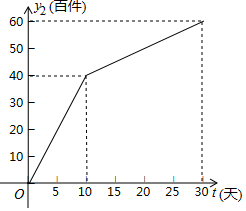 我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.| 时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量 y1(百件) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2与-$\frac{1}{2}$ | B. | 2与|-2| | C. | -2与$\root{3}{-8}$ | D. | -2与$\sqrt{(-2)^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com