
【题目】如图,BF和CE分别是钝角△ABC(∠ABC是钝角)中AC、AB边上的中线,又BF⊥CE,垂足是G,过点G作GH⊥BC,垂足为H.
(1)求证:GH2=BHCH;
(2)若BC=20,并且点G到BC的距离是6,则AB的长为多少?

【答案】(1)证明见解析(2)2![]()
【解析】
(1)只要证明△CGH∽△GBH即可解决问题;
(2)作EM⊥CB交CB的延长线于M.设CH=x,HB=y.构建方程组求出x、y,解直角三角形求出EM、BM即可.
(1)证明:∵CE⊥BF,GH⊥BC,
∴∠CGB=∠CHG=∠BHG=90°,
∴∠CGH+∠BGH=90°,∠BGH+∠GBH=90°,
∴∠CGH=∠GBH,
∴△CGH∽△GBH,
∴![]() ,
,
∴GH2=BHCH;
(2)解:作EM⊥CB交CB的延长线于M.设CH=x,HB=y.

则有![]() ,解得
,解得![]() 或
或![]() ,
,
∵∠ABC是钝角,
∴CH>BH,
∴CH=18,BH=2,
∵G是△ABC的重心,∴CG=2EG,
∵GH⊥BC,EM⊥BC,
∴GH∥EM,
∴![]() ,
,
∴EM=9,CM=27,
∴BM=CM﹣BC=7,
∴BE=![]() ,
,
∴AB=2BE=2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
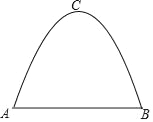
【题目】一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数y2=![]() (m<0)图象的两个交点,AC⊥x轴于C.
(m<0)图象的两个交点,AC⊥x轴于C.

(1)求出k,b及m的值.
(2)根据图象直接回答:在第二象限内,当y1>y2时,x的取值范围是 ________.
(3)若P是线段AB上的一点,连接PC,若△PCA的面积等于![]() ,求点P坐标.
,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图像,假设两种灯的使用寿命都是2000h,照明效果一样.
(1)根据图像分别求出L1,L2的函数关系式.
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在相同条件下完成了10次射击训练,两人的成绩如图所示。

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 方差/环 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根据训练成绩,你认为选派哪一名队员参赛更好?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,且点
两点,且点![]() 的横坐标和点
的横坐标和点![]() 的纵坐标都是
的纵坐标都是![]() ,求:
,求:

![]() 一次函数的解析式;(2)
一次函数的解析式;(2)![]() 的面积.
的面积.
![]() 根据图象回答:当
根据图象回答:当![]() 为何值时,一次函数的函数值大于反比例函数的函数值.
为何值时,一次函数的函数值大于反比例函数的函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
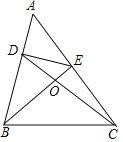
【题目】(1)如图,在△ABC中,∠A是锐角,点D,E分别在AB,AC上,且∠DCB=∠EBC=![]() ∠A,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
∠A,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
(2)已知四边形ABCD,连接AC、BD交于O,且满足条件:AB+CD=AD+BC,AB2+AD2=BC2+DC2,请探究AC与BD的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com