
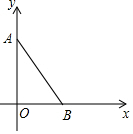 如图,平面直角坐标系xOy中,已知点A(0,3),点B($\sqrt{3}$,0),连接AB,若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
如图,平面直角坐标系xOy中,已知点A(0,3),点B($\sqrt{3}$,0),连接AB,若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.分析 (1)直接利用线段AB的“等长点”的条件判断;
(2)分两种情况讨论,利用对称性和垂直的性质即可求出m,n;
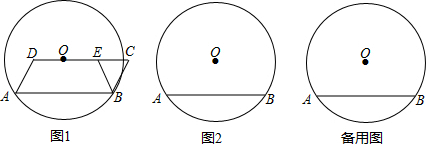
(3)先判断出直线y=kx+3$\sqrt{3}$与圆A,B相切时,如图2所示,利用相似三角形的性质即可求出结论.
解答 解:(1)∵A(0,3),B($\sqrt{3}$,0),
∴AB=2$\sqrt{3}$,
∵点C1(-2,3+2$\sqrt{2}$),
∴AC1=$\sqrt{4+8}$=2$\sqrt{3}$,
∴AC1=AB,
∴C1是线段AB的“等长点”,
∵点C2(0,-2),
∴AC2=5,BC2=$\sqrt{3+4}$=$\sqrt{7}$,
∴AC2≠AB,BC2≠AB,
∴C2不是线段AB的“等长点”,
∵点C3(3+$\sqrt{3}$,-$\sqrt{3}$),
∴BC3=$\sqrt{9+3}$=2$\sqrt{3}$,
∴BC3=AB,
∴C3是线段AB的“等长点”;
故答案为:C1,C3;
(2)如图1,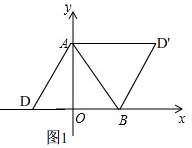 在Rt△AOB中,OA=3,OB=$\sqrt{3}$,
在Rt△AOB中,OA=3,OB=$\sqrt{3}$,
∴AB=2$\sqrt{3}$,tan∠OAB=$\frac{OB}{OA}$=$\frac{\sqrt{3}}{3}$,
∴∠OAB=30°,
当点D在y轴左侧时,
∵∠DAB=60°,
∴∠DAO=∠DAB-∠BAO=30°,
∵点D(m,n)是线段AB的“等长点”,
∴AD=AB,
∴D(-$\sqrt{3}$,0),
∴m=$\sqrt{3}$,n=0,
当点D在y轴右侧时,
∵∠DAB=60°,
∴∠DAO=∠BAO+∠DAB=90°,
∴n=3,
∵点D(m,n)是线段AB的“等长点”,
∴AD=AB=2$\sqrt{3}$,
∴m=2$\sqrt{3}$;
(3)如图2,∵直线y=kx+3$\sqrt{3}$k=k(x+3$\sqrt{3}$),
∴直线y=kx+3$\sqrt{3}$k恒过一点P(-3$\sqrt{3}$,0),
∴在Rt△AOP中,OA=3,OP=3$\sqrt{3}$,
∴∠APO=30°,
∴∠OPA=60°,
∴∠BAP=90°, 当PF与⊙B相切时交y轴于F,
当PF与⊙B相切时交y轴于F,
∴PA切⊙B于A,
∴点F就是直线y=kx+3$\sqrt{3}$k与⊙B的切点,
∴F(0,-3),
∴3$\sqrt{3}$k=-3,
∴k=-$\frac{\sqrt{3}}{3}$,
当直线y=kx+3$\sqrt{3}$k与⊙A相切时交y轴于G切点为E,∴∠AEG=∠OPG=90°,
∴△AEG∽△POG,
∴$\frac{AE}{OP}=\frac{AG}{PG}$,
∴$\frac{2\sqrt{3}}{3\sqrt{3}}=\frac{3\sqrt{3}k-3}{3\sqrt{{k}^{2}+3}}$,
∴k=$\frac{3\sqrt{3}-4\sqrt{2}}{5}$(舍)或k=$\frac{3\sqrt{3}+4\sqrt{2}}{5}$,
∵直线y=kx+3$\sqrt{3}$k上至少存在一个线段AB的“等长点”,
∴-$\frac{\sqrt{3}}{3}$≤k≤$\frac{3\sqrt{3}+4\sqrt{2}}{5}$.
点评 此题是一次函数综合题,主要考查了新定义,锐角三角函数,直角三角形的性质,等腰三角形的性质,对称性,解(1)的关键是理解新定义,解(2)的关键是画出图形,解(3)的关键是判断出直线和圆A,B相切时是分界点,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:选择题
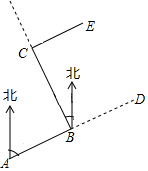 如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )| A. | 80° | B. | 90° | C. | 100° | D. | 105° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
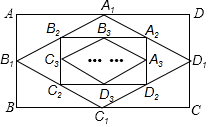 如图,顺次连接矩形ABCD四边的中点得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得到四边形A3B3C3D3,…,已知AB=6,BC=8,按此方法得到的四边形A5B5C5D5的周长为5.
如图,顺次连接矩形ABCD四边的中点得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得到四边形A3B3C3D3,…,已知AB=6,BC=8,按此方法得到的四边形A5B5C5D5的周长为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
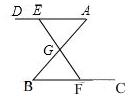 如图,在△ABC中,BC=4cm,过点A作射线AD∥BC,点E从点A出发沿射线AD以1cm/s的速度运动.同时点F从点B出发沿射线BC以1cm/s速度运动,连结EF交AB于点G,设点E运动时间为t(s).
如图,在△ABC中,BC=4cm,过点A作射线AD∥BC,点E从点A出发沿射线AD以1cm/s的速度运动.同时点F从点B出发沿射线BC以1cm/s速度运动,连结EF交AB于点G,设点E运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com