
 如图,一艘海轮位于灯塔P的北偏西80°方向的A处,它以每小时45海里的速度向正南方向航行,2小时后到达位于灯塔P的南偏西20°的B处,则B处与灯塔P的距离为( )
如图,一艘海轮位于灯塔P的北偏西80°方向的A处,它以每小时45海里的速度向正南方向航行,2小时后到达位于灯塔P的南偏西20°的B处,则B处与灯塔P的距离为( )| A. | 45海里 | B. | 60海里 | C. | 70海里 | D. | 90海里 |
分析 根据平行线的性质可以得出∠ABP=20°,根据角的运算即可得出∠BAP=80°=∠APB,从而得出BP=AB,再根据“路程=速度×时间”即可得出结论.
解答 解:在图中标上字母,如图所示.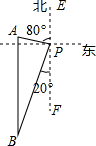
∵海轮从点A往正南方向航行,
∴AB∥EF,
∴∠ABP=∠BPF=20°.
∵∠APB=180°-∠APE-∠BPF=180°-80°-20°=80°,
∴∠BAP=180°-∠ABP-∠APB=80°,
∴BP=AB=45×2=/0(海里).
故选D.
点评 本题考查了等腰三角形的判定以及平行线的性质,解题的关键是找出△ABP为等腰三角形.本题属于基础题,难度不大,解该题型题目时,根据平行线的性质找出相等的角是关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{28}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com