
 已知:(
已知:(| 1 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2010 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2010(1+2010) |
| 2 |
| 2021055 |
| 4 |
| ||
| 2 |
| 2010 |


科目:初中数学 来源: 题型:
 景区大楼AB段上有四处居民小区A,B,C,D,且有AC=CD=DB,为改善居民购物的环境,要在AB路建一家超市,每个小区的居民各执一词,难以确定超市的位置,如果由你出任超市负责人,以便民、获利的角度考虑,你将把超市建在哪儿?
景区大楼AB段上有四处居民小区A,B,C,D,且有AC=CD=DB,为改善居民购物的环境,要在AB路建一家超市,每个小区的居民各执一词,难以确定超市的位置,如果由你出任超市负责人,以便民、获利的角度考虑,你将把超市建在哪儿?查看答案和解析>>
科目:初中数学 来源: 题型:
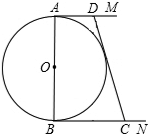 如图,⊙0的直径AB=2,AM和BN是它的两条切线,且AD+BC=CD,连OD,OC,
如图,⊙0的直径AB=2,AM和BN是它的两条切线,且AD+BC=CD,连OD,OC,查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、有两个相等的实数根 |
| B、有两个不相等的实数根 |
| C、没有实数根 |
| D、无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com